Coupled channel Riemann sheets#
Import Python libraries
# @title
from __future__ import annotations
import os
import warnings
from typing import Any
import matplotlib.pyplot as plt
import numpy as np
import plotly.graph_objects as go
import sympy as sp
from ampform.io import aslatex
from ampform.kinematics.phasespace import Kallen
from ampform.sympy import unevaluated
from IPython.display import Math, display
from ipywidgets import widgets as w
from plotly.colors import DEFAULT_PLOTLY_COLORS
from plotly.subplots import make_subplots
warnings.filterwarnings("ignore")
Expression definitions#
Show code cell source
# @title
@unevaluated(real=False)
class PhaseSpaceFactor(sp.Expr):
s: Any
m1: Any
m2: Any
_latex_repr_ = R"\rho_{{{m1}, {m2}}}\left({s}\right)"
def evaluate(self) -> sp.Expr:
s, m1, m2 = self.args
return sp.sqrt((s - ((m1 + m2) ** 2)) * (s - (m1 - m2) ** 2) / s**2)
s, m1, m2 = sp.symbols("s m1 m2")
rho_expr = PhaseSpaceFactor(s, m1, m2)
Math(aslatex({rho_expr: rho_expr.doit(deep=False)}))
Show code cell source
# @title
@unevaluated(real=False)
class PhaseSpaceFactorKallen(sp.Expr):
s: Any
m1: Any
m2: Any
_latex_repr_ = R"\rho_{{{m1}, {m2}}}\left({s}\right)"
def evaluate(self) -> sp.Expr:
s, m1, m2 = self.args
return 2 * BreakupMomentum(s, m1, m2) / sp.sqrt(s)
@unevaluated(real=False)
class PhaseSpaceCM(sp.Expr):
s: Any
m1: Any
m2: Any
_latex_repr_ = R"\rho^\mathrm{{CM}}_{{{m1},{m2}}}\left({s}\right)"
def evaluate(self) -> sp.Expr:
s, m1, m2 = self.args
return -16 * sp.pi * sp.I * ChewMandelstam(s, m1, m2)
@unevaluated(real=False)
class ChewMandelstam(sp.Expr):
s: Any
m1: Any
m2: Any
_latex_repr_ = R"\Sigma\left({s}\right)"
def evaluate(self) -> sp.Expr:
s, m1, m2 = self.args
q = BreakupMomentum(s, m1, m2)
return (
1
/ (16 * sp.pi**2)
* (
(2 * q / sp.sqrt(s))
* sp.log((m1**2 + m2**2 - s + 2 * sp.sqrt(s) * q) / (2 * m1 * m2))
- (m1**2 - m2**2) * (1 / s - 1 / (m1 + m2) ** 2) * sp.log(m1 / m2)
)
)
@unevaluated(real=False)
class BreakupMomentum(sp.Expr):
s: Any
m1: Any
m2: Any
_latex_repr_ = R"q\left({s}\right)"
def evaluate(self) -> sp.Expr:
s, m1, m2 = self.args
return sp.sqrt(Kallen(s, m1**2, m2**2)) / (2 * sp.sqrt(s))
s, m1, m2 = sp.symbols("s m1 m2")
rho_expr_kallen = PhaseSpaceFactorKallen(s, m1, m2)
rho_cm_expr = PhaseSpaceCM(s, m1, m2)
cm_expr = ChewMandelstam(s, m1, m2)
q_expr = BreakupMomentum(s, m1, m2)
kallen = Kallen(*sp.symbols("x:z"))
Math(
aslatex({
e: e.doit(deep=False)
for e in [rho_expr_kallen, rho_cm_expr, cm_expr, q_expr, kallen]
})
)
Riemann sheet I#
Matrix definition#
Show code cell source
# @title
class DiagonalMatrix(sp.DiagonalMatrix):
def _latex(self, printer, *args):
return printer._print(self.args[0])
n = 2
I = sp.Identity(n)
K = sp.MatrixSymbol("K", n, n)
CM = DiagonalMatrix(sp.MatrixSymbol(R"\rho^\Sigma", n, n))
Math(aslatex({CM: CM.as_explicit()}))
T_I_explicit = T_I.as_explicit()
T_I_explicit[0, 0].simplify(doit=False)
Parametrization#
Symbol definitions
Show code cell source
# @title
k_expr_00 = (g1 * g1 * m0) / (s - m0**2)
k_expr_10 = (g1 * g2 * m0) / (s - m0**2)
k_expr_11 = (g2 * g2 * m0) / (s - m0**2)
cm_expressions = {
K[0, 0]: k_expr_00,
K[1, 1]: k_expr_11,
K[0, 1]: k_expr_10,
K[1, 0]: k_expr_10,
CM[0, 0]: -PhaseSpaceCM(s, ma1, mb1),
CM[1, 1]: -PhaseSpaceCM(s, ma2, mb2),
}
Math(aslatex(cm_expressions))
T_I_cm_expr = T_I_explicit.xreplace(cm_expressions)
T_I_cm_expr[0, 0].simplify(doit=False)
Sheets II, III, and IV#
In the case of two channels, there are four Riemann sheets. The first sheet (Sheet I) is physical and three unphysical ones. The physical sheet is calculated using the analytic solution of the Chew-Mandelstam function.
Depending on the centre-of-mass energy, different Riemann sheets connect smoothly to the physical one. Therefore, two cases are studied: one where the resonance mass is above the threshold of the second and first channel, and another where the resonance mass is between the threshold of the first and second channel.
Show code cell source
# @title
rho = DiagonalMatrix(sp.MatrixSymbol("rho", n, n))
Math(aslatex({rho: rho.as_explicit()}))
T_II_explicit = T_II.as_explicit()
T_II_explicit[0, 0].simplify(doit=False)
T_III_explicit = T_III.as_explicit()
T_III_explicit[0, 0].simplify(doit=False)
T_IV_explicit = T_IV.as_explicit()
T_IV_explicit[0, 0].simplify(doit=False)
rho_expressions_II = {
**cm_expressions,
rho[0, 0]: PhaseSpaceFactor(s, ma1, mb1),
rho[1, 1]: 0,
}
rho_expressions_III = {
**cm_expressions,
rho[0, 0]: PhaseSpaceFactor(s, ma1, mb1),
rho[1, 1]: PhaseSpaceFactor(s, ma2, mb2),
}
rho_expressions_IV = {
**cm_expressions,
rho[0, 0]: 0,
rho[1, 1]: PhaseSpaceFactor(s, ma2, mb2),
}
# @title
T_II_rho_expr = T_II_explicit.xreplace(rho_expressions_II)
T_III_rho_expr = T_III_explicit.xreplace(rho_expressions_III)
T_IV_rho_expr = T_IV_explicit.xreplace(rho_expressions_IV)
T_II_rho_expr[0, 0].simplify(doit=False)
T_III_rho_expr[0, 0].simplify(doit=False)
Visualizations#
Lineshapes (real axis)#
Show code cell source
# @title
%config InlineBackend.figure_formats = ["svg"]
T_I_func = sp.lambdify(symbols, T_I_cm_expr[0, 0].doit())
T_II_func = sp.lambdify(symbols, T_II_rho_expr[0, 0].doit())
T_III_func = sp.lambdify(symbols, T_III_rho_expr[0, 0].doit())
T_IV_func = sp.lambdify(symbols, T_IV_rho_expr[0, 0].doit())
parameter_defaults1 = {
ma1: 1.0,
mb1: 1.5,
ma2: 1.5,
mb2: 2.0,
m0: 4.0,
g1: 0.7,
g2: 0.7,
}
parameter_defaults2 = {
**parameter_defaults1,
m0: 3.0,
}
args1 = eval(str(symbols[1:].xreplace(parameter_defaults1)))
args2 = eval(str(symbols[1:].xreplace(parameter_defaults2)))
epsilon = 1e-5
x = np.linspace(0, 8, num=300)
y = np.linspace(epsilon, 1, num=100)
X, Y = np.meshgrid(x, y)
Zn = X - Y * 1j
Zp = X + Y * 1j
T1n_res1 = T_I_func(Zn**2, *args1)
T1p_res1 = T_I_func(Zp**2, *args1)
T2n_res1 = T_II_func(Zn**2, *args1)
T2p_res1 = T_II_func(Zp**2, *args1)
T3n_res1 = T_III_func(Zn**2, *args1)
T3p_res1 = T_III_func(Zp**2, *args1)
T4n_res1 = T_IV_func(Zn**2, *args1)
T4p_res1 = T_IV_func(Zp**2, *args1)
T1n_res2 = T_I_func(Zn**2, *args2)
T1p_res2 = T_I_func(Zp**2, *args2)
T2n_res2 = T_II_func(Zn**2, *args2)
T2p_res2 = T_II_func(Zp**2, *args2)
T3n_res2 = T_III_func(Zn**2, *args2)
T3p_res2 = T_III_func(Zp**2, *args2)
T4n_res2 = T_IV_func(Zn**2, *args2)
T4p_res2 = T_IV_func(Zp**2, *args2)
fig, axes = plt.subplots(figsize=(11, 6), ncols=4, sharey=True)
ax1, ax2, ax3, ax4 = axes.flatten()
ax1.plot(x, T1n_res1[0].imag, label=R"$T_\mathrm{I}(s-0i)$")
ax1.plot(x, T1p_res1[0].imag, label=R"$T_\mathrm{I}(s+0i)$")
ax1.set_title(f"${sp.latex(rho_cm_expr)}$")
ax1.set_title(R"$T_\mathrm{I}$")
ax2.plot(x, T2n_res1[0].imag, label=R"$T_\mathrm{II}(s-0i)$")
ax2.plot(x, T2p_res1[0].imag, label=R"$T_\mathrm{II}(s+0i)$")
ax2.set_title(R"$T_\mathrm{II}$")
ax3.plot(x, T3n_res1[0].imag, label=R"$T_\mathrm{III}(s-0i)$")
ax3.plot(x, T3p_res1[0].imag, label=R"$T_\mathrm{III}(s+0i)$")
ax3.set_title(R"$T_\mathrm{III}$")
ax4.plot(x, T4n_res1[0].imag, label=R"$T_\mathrm{III}(s-0i)$")
ax4.plot(x, T4p_res1[0].imag, label=R"$T_\mathrm{IV}(s+0i)$")
ax4.set_title(R"$T_\mathrm{III}$")
for ax in axes:
ax.legend()
ax.set_xlabel(R"$\mathrm{Re}\,\sqrt{s}$")
ax.set_ylim(-1, +1)
ax1.set_ylabel(R"$\mathrm{Im}\,T(s)$ (a.u.)")
fig.tight_layout()
plt.show()
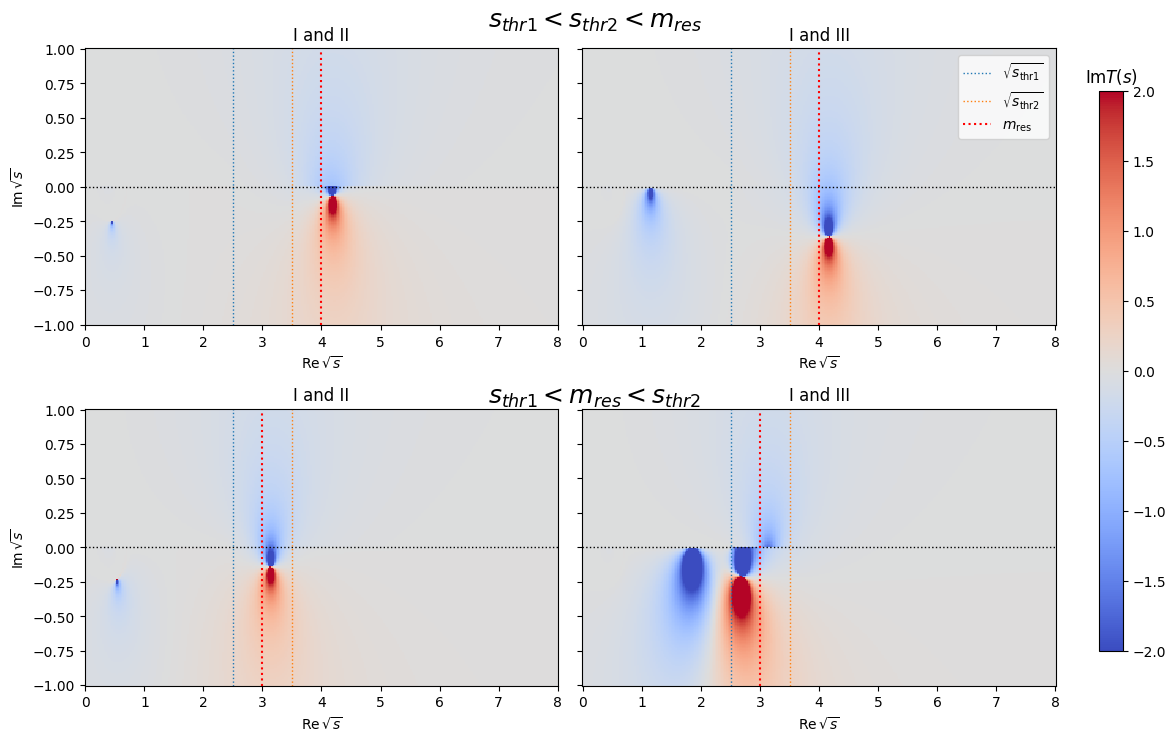
Complex plane (2D)#
It can be shown that if the resonance mass is above both thresholds the third sheet connects smoothly to the first sheet. If the resonance mass is above the first and below the second threshold the second sheet transitions smoothly into the first sheet.
Show code cell source
# @title
%config InlineBackend.figure_formats = ["png"]
fig, axes = plt.subplots(figsize=(12, 8), ncols=2, nrows=2, sharey=True)
ax1, ax2, ax3, ax4 = axes.flatten()
for ax in axes.flatten():
ax.set_xlabel(R"$\mathrm{Re}\,\sqrt{s}$")
for ax in axes[:, 0]:
ax.set_ylabel(R"$\mathrm{Im}\,\sqrt{s}$")
ax1.set_title("I and II")
ax2.set_title("I and III")
ax3.set_title("I and II")
ax4.set_title("I and III")
T_max = 2
style = dict(vmin=-T_max, vmax=+T_max, cmap=plt.cm.coolwarm)
mesh = ax1.pcolormesh(X, Y, T1p_res1.imag, **style)
ax1.pcolormesh(X, -Y, T2n_res1.imag, **style)
ax2.pcolormesh(X, +Y, T1p_res1.imag, **style)
ax2.pcolormesh(X, -Y, T3n_res1.imag, **style)
ax3.pcolormesh(X, +Y, T1p_res2.imag, **style)
ax3.pcolormesh(X, -Y, T2n_res2.imag, **style)
ax4.pcolormesh(X, +Y, T1p_res2.imag, **style)
ax4.pcolormesh(X, -Y, T3n_res2.imag, **style)
s_thr1 = parameter_defaults1[ma1] + parameter_defaults1[mb1]
s_thr2 = parameter_defaults1[ma2] + parameter_defaults1[mb2]
linestyle = dict(ls="dotted", lw=1)
for ax in axes.flatten():
ax.axhline(0, c="black", **linestyle)
ax.axvline(s_thr1, c="C0", **linestyle, label=R"$\sqrt{s_\mathrm{thr1}}$")
ax.axvline(s_thr2, c="C1", **linestyle, label=R"$\sqrt{s_\mathrm{thr2}}$")
linestyle = dict(c="r", ls="dotted", label=R"$m_\mathrm{res}$")
for ax in axes[0]:
ax.axvline(parameter_defaults1[m0], **linestyle)
for ax in axes[1]:
ax.axvline(parameter_defaults2[m0], **linestyle)
ax2.legend()
fig.text(0.5, 0.93, R"$s_{thr1}<s_{thr2}<m_{res}$", ha="center", fontsize=18)
fig.text(0.5, 0.46, R"$s_{thr1}<m_{res}<s_{thr2}$", ha="center", fontsize=18)
fig.subplots_adjust(wspace=1)
cax = fig.add_axes([0.92, 0.15, 0.02, 0.7])
cbar = fig.colorbar(mesh, cax=cax)
cbar.ax.set_title(R"$\mathrm{Im} T(s)$")
fig.tight_layout(rect=[0, 0.03, 0.9, 0.95])
fig.show()
Riemann sheets (3D)#
Define plot style
# @title
def sty(sheet_name: str) -> dict:
sheet_color = sheet_colors[sheet_name]
n_lines = 16
return dict(
cmin=-vmax,
cmax=+vmax,
colorscale=[[0, "rgb(0, 0, 0)"], [1, sheet_color]],
contours=dict(
x=dict(
show=True,
start=x.min(),
end=x.max(),
size=(x.max() - x.min()) / n_lines,
color="black",
),
y=dict(
show=True,
start=-y.max(),
end=+y.max(),
size=(y.max() - y.min()) / (n_lines // 2),
color="black",
),
),
name=sheet_name,
opacity=0.4,
showscale=False,
)
vmax = 2.0
project = np.imag
sheet_colors = {
"T1 (physical)": "blue",
"T2 (unphysical)": "red",
"T3 (unphysical)": "green",
"T4 (unphysical)": "yellow",
}
Show code cell source
# @title
Sp_I_res1 = go.Surface(x=X, y=+Y, z=T1p_res1.imag, **sty("T1 (physical)"))
Sn_II_res1 = go.Surface(x=X, y=-Y, z=T2n_res1.imag, **sty("T2 (unphysical)"))
Sn_III_res1 = go.Surface(x=X, y=-Y, z=T3n_res1.imag, **sty("T3 (unphysical)"))
Sp_I_res2 = go.Surface(x=X, y=+Y, z=T1p_res2.imag, **sty("T1 (physical)"))
Sn_II_res2 = go.Surface(x=X, y=-Y, z=T2n_res2.imag, **sty("T2 (unphysical)"))
Sn_III_res2 = go.Surface(x=X, y=-Y, z=T3n_res2.imag, **sty("T3 (unphysical)"))
thr1_filter = x >= s_thr1
thr2_filter = x >= s_thr2
line_kwargs = dict(
line=dict(color="yellow", width=8),
mode="lines",
name="Lineshape",
)
lineshape_res1_z = project(T1p_res1[0])
lineshape_res2_z = project(T1p_res2[0])
lineshape_res1 = go.Scatter3d(
x=x[thr1_filter],
y=np.zeros(thr1_filter.shape),
z=lineshape_res1_z[thr1_filter],
**line_kwargs,
)
lineshape_res2 = go.Scatter3d(
x=x[thr1_filter],
y=np.zeros(thr1_filter.shape),
z=lineshape_res2_z[thr1_filter],
**line_kwargs,
)
point_kwargs = dict(
hoverinfo="text",
marker=dict(color=DEFAULT_PLOTLY_COLORS[:2], size=6),
mode="markers",
text=["threshold 1", "threshold 2"],
)
thr_points_res1 = go.Scatter3d(
x=[s_thr1, s_thr2],
y=[0, 0],
z=[lineshape_res1_z[thr1_filter][0], lineshape_res1_z[thr2_filter][0]],
**point_kwargs,
)
thr_points_res2 = go.Scatter3d(
x=[s_thr1, s_thr2],
y=[0, 0],
z=[lineshape_res2_z[thr1_filter][0], lineshape_res2_z[thr2_filter][0]],
**point_kwargs,
)
plotly_fig = make_subplots(
rows=2,
cols=2,
horizontal_spacing=0.01,
vertical_spacing=0.05,
specs=[
[{"type": "surface"}, {"type": "surface"}],
[{"type": "surface"}, {"type": "surface"}],
],
subplot_titles=[
"thr₁ < thr₂ < mᵣ",
"thr₁ < mᵣ < thr₂",
],
)
# thr₁ < thr₂ < mᵣ
selector = dict(col=1, row=1)
plotly_fig.add_trace(Sp_I_res1, **selector)
plotly_fig.add_trace(Sn_III_res1, **selector)
plotly_fig.add_trace(lineshape_res1, **selector)
plotly_fig.add_trace(thr_points_res1, **selector)
selector = dict(col=1, row=2)
plotly_fig.add_trace(Sp_I_res1, **selector)
plotly_fig.add_trace(Sn_II_res1, **selector)
plotly_fig.add_trace(lineshape_res1, **selector)
plotly_fig.add_trace(thr_points_res1, **selector)
# thr₁ < mᵣ < thr₂
selector = dict(col=2, row=1)
plotly_fig.add_trace(Sp_I_res2, **selector)
plotly_fig.add_trace(Sn_II_res2, **selector)
plotly_fig.add_trace(lineshape_res2, **selector)
plotly_fig.add_trace(thr_points_res2, **selector)
selector = dict(col=2, row=2)
plotly_fig.add_trace(Sp_I_res2, **selector)
plotly_fig.add_trace(Sn_III_res2, **selector)
plotly_fig.add_trace(lineshape_res2, **selector)
plotly_fig.add_trace(thr_points_res2, **selector)
plotly_fig.update_layout(
height=600,
margin=dict(l=0, r=0, t=20, b=0),
showlegend=False,
)
plotly_fig.update_scenes(
camera_center=dict(z=-0.1),
camera_eye=dict(x=1.4, y=1.4, z=1.4),
xaxis_range=(2.0, 5.0),
xaxis_title_text="Re √s",
yaxis_title_text="Im √s",
zaxis_title_text="Im T(s)",
zaxis_range=[-vmax, +vmax],
)
plotly_fig.show()



