Classes | |
| struct | InputInfo |
Typedefs | |
| using | BreitWignerFunction = std::function< std::complex< double >(double, double, double, double, double, unsigned int, double, std::shared_ptr< FormFactor >)> |
Functions | |
| std::complex< double > | relativisticBreitWigner (double mSq, double mR, double ma, double mb, double width, unsigned int L, double mesonRadius, std::shared_ptr< FormFactor > FormFactorFunctor) |
| Relativistic Breit-Wigner model with barrier factors. More... | |
| std::complex< double > | relativisticBreitWignerAnalyticCont (double mSq, double mR, double ma, double mb, double width, unsigned int L, double mesonRadius, std::shared_ptr< FormFactor > FormFactorFunctor) |
| Relativistic Breit-Wigner model with barrier factors. More... | |
| std::shared_ptr< ComPWA::FunctionTree::TreeNode > | createFunctionTree (InputInfo Params, std::shared_ptr< ComPWA::FunctionTree::Value< std::vector< double >>> InvMassSquared) |
Typedef Documentation
◆ BreitWignerFunction
| using ComPWA::Physics::Dynamics::RelativisticBreitWigner::BreitWignerFunction = typedef std::function<std::complex<double>( double, double, double, double, double, unsigned int, double, std::shared_ptr<FormFactor>)> |
Definition at line 39 of file RelativisticBreitWigner.hpp.
Function Documentation
◆ createFunctionTree()
| std::shared_ptr< TreeNode > ComPWA::Physics::Dynamics::RelativisticBreitWigner::createFunctionTree | ( | RelativisticBreitWigner::InputInfo | Params, |
| std::shared_ptr< ComPWA::FunctionTree::Value< std::vector< double >>> | InvMassSquared | ||
| ) |
Definition at line 17 of file RelativisticBreitWigner.cpp.
◆ relativisticBreitWigner()
|
inline |
Relativistic Breit-Wigner model with barrier factors.
The dynamical function implemented here is taken from PDG2018 (Eq.48.22) for the one channel case. The dynamic reaction
![\[ \mathcal{A}_R(s) = \frac{g_p*g}{s - M_R^2 + i \sqrt{s} \Gamma_R B^2} \]](form_12.png)
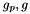 are the coupling constants for production and decay and the barrier term
are the coupling constants for production and decay and the barrier term 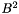 is parameterized according to Eq.48.23:
is parameterized according to Eq.48.23:
![\[ B^2 = \left( \frac{q(\sqrt{s})}{q(M_R)} \right)^{2L+1} \times \left( \frac{M_R}{\sqrt{s}} \right) \times \left( \frac{F(\sqrt{s})}{F(\sqrt{s_R})} \right)^{2} \]](form_15.png)
This corresponds to the Blatt Weisskopf form factors B_L like
![\[ B^2 = \left( \frac{q(\sqrt{s})}{q(M_R)} \right) \times \left( \frac{M_R}{\sqrt{s}} \right) \times \left( \frac{B_L(\sqrt{s})}{B_L(\sqrt{s_R})} \right)^{2} \]](form_16.png)
- Parameters
-
mSq Invariant mass squared mR Mass of the resonant state ma Mass of daughter particle mb Mass of daughter particle width Decay width L Orbital angular momentum between two daughters a and b mesonRadius Meson Radius FormFactorFunctor Form factor functor
- Returns
- Amplitude value
Definition at line 77 of file RelativisticBreitWigner.hpp.
◆ relativisticBreitWignerAnalyticCont()
|
inline |
Relativistic Breit-Wigner model with barrier factors.
The dynamical function implemented here is taken from PDG2018 (Eq.48.22) for the one channel case. The dynamic reaction
![\[ \mathcal{A}_R(s) = \frac{g_p*g}{s - M_R^2 + i \sqrt{s} \Gamma_R B^2} \]](form_12.png)
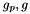 are the coupling constants for production and decay and the barrier term
are the coupling constants for production and decay and the barrier term 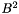 is parameterized according to Eq.48.23:
is parameterized according to Eq.48.23:
![\[ B^2 = \left( \frac{q(\sqrt{s})}{q(M_R)} \right)^{2L+1} \times \left( \frac{M_R}{\sqrt{s}} \right) \times \left( \frac{F(\sqrt{s})}{F(\sqrt{s_R})} \right)^{2} \]](form_15.png)
This corresponds to the Blatt Weisskopf form factors B_L like
![\[ B^2 = \left( \frac{q(\sqrt{s})}{q(M_R)} \right) \times \left( \frac{M_R}{\sqrt{s}} \right) \times \left( \frac{B_L(\sqrt{s})}{B_L(\sqrt{s_R})} \right)^{2} \]](form_16.png)
- Parameters
-
mSq Invariant mass squared mR Mass of the resonant state ma Mass of daughter particle mb Mass of daughter particle width Decay width L Orbital angular momentum between two daughters a and b mesonRadius Meson Radius FormFactorFunctor Form factor functor
- Returns
- Amplitude value
Definition at line 145 of file RelativisticBreitWigner.hpp.
