Amplitude model with ampform

Formulate helicity amplitude model for \(p \gamma \to \eta \pi^0 p\) symbolically using AmpForm.

Import Python libraries

Hide code cell source

import logging
import os
import warnings
from collections import defaultdict

import ampform
import graphviz
import ipywidgets as w
import jax
import jax.numpy as jnp
import matplotlib.pyplot as plt
import numpy as np
import qrules
import sympy as sp
from ampform.dynamics.builder import RelativisticBreitWignerBuilder
from ampform.io import aslatex, improve_latex_rendering
from IPython.display import SVG, Image, Math, display
from qrules.particle import Particle, Spin, create_particle, load_pdg
from tensorwaves.data import (
    SympyDataTransformer,
    TFPhaseSpaceGenerator,
    TFUniformRealNumberGenerator,
)
from tensorwaves.function.sympy import create_parametrized_function

STATIC_PAGE = "EXECUTE_NB" in os.environ

os.environ["TF_CPP_MIN_LOG_LEVEL"] = "3"
logging.disable(logging.WARNING)
warnings.filterwarnings("ignore")

improve_latex_rendering()
particle_db = load_pdg()

Generate transitions

pgamma1 = Particle(
    name="pgamma1",
    latex=r"p\gamma (s1/2)",
    spin=0.5,
    mass=4.101931071854584,
    charge=1,
    isospin=Spin(1 / 2, +1 / 2),
    baryon_number=1,
    parity=-1,
    pid=99990,
)
pgamma2 = create_particle(
    template_particle=pgamma1,
    name="pgamma2",
    latex=R"p\gamma (s3/2)",
    spin=1.5,
    pid=pgamma1.pid + 1,
)
particle_db.update([pgamma1, pgamma2])

We keep the relevant information about branching fractions in the previous Branching fraction chapter. For simplicity, after the information about branching fraction, and under the current qrules results, we limit the intermediate resonances to be:

• \(a(2)\) for \(\eta \pi^0\),

• \(\Delta(1232)\) for \(\pi p\)”,

• and “\(N(1535)\)” for both \(\pi^0 p\) and \(\eta p\).

reaction = qrules.generate_transitions(
    initial_state="pgamma1",
    final_state=["eta", "pi0", "p"],
    allowed_intermediate_particles=["a(2)(1320)", "N(1535)", "Delta(1232)"],
    allowed_interaction_types=["strong", "EM"],
    particle_db=particle_db,
    max_angular_momentum=3,
    max_spin_magnitude=3,
    mass_conservation_factor=0,
)

Show code cell source

Hide code cell source

src = qrules.io.asdot(reaction, collapse_graphs=True)
graphviz.Source(src)

Formulate model

model_builder = ampform.get_builder(reaction)
model_builder.config.scalar_initial_state_mass = True
model_builder.config.stable_final_state_ids = 0, 1, 2
bw_builder = RelativisticBreitWignerBuilder(
    energy_dependent_width=False,
    form_factor=False,
)
for name in reaction.get_intermediate_particles().names:
    model_builder.dynamics.assign(name, bw_builder)
model = model_builder.formulate()

The first component of the full amplitude is shown below. The other terms are in similar way of formualation and thus not showing explicitly here again.

Show code cell source

Hide code cell source

(symbol, expr), *_ = model.amplitudes.items()
Math(aslatex({symbol: expr}, terms_per_line=1))

\[\begin{split}\displaystyle \begin{aligned} A^{01}_{- \frac{1}{2}, 0, 0, - \frac{1}{2}} \;&=\; \frac{C_{p\gamma (s1/2) \xrightarrow[S=3/2]{L=1} a_{2}(1320)^{0} p; a_{2}(1320)^{0} \xrightarrow[S=0]{L=2} \eta \pi^{0}} \Gamma_{a_{2}(1320)^{0}} m_{a_{2}(1320)^{0}} C^{0,0}_{0,0,0,0} C^{\frac{1}{2},- \frac{1}{2}}_{1,0,\frac{3}{2},- \frac{1}{2}} C^{\frac{3}{2},- \frac{1}{2}}_{2,-1,\frac{1}{2},\frac{1}{2}} C^{2,0}_{2,0,0,0} D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{2}_{-1,0}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{a_{2}(1320)^{0}} m_{a_{2}(1320)^{0}} - m_{01}^{2} + \left(m_{a_{2}(1320)^{0}}\right)^{2}} \\ \;&+\; \frac{C_{p\gamma (s1/2) \xrightarrow[S=3/2]{L=1} a_{2}(1320)^{0} p; a_{2}(1320)^{0} \xrightarrow[S=0]{L=2} \eta \pi^{0}} \Gamma_{a_{2}(1320)^{0}} m_{a_{2}(1320)^{0}} C^{0,0}_{0,0,0,0} C^{\frac{1}{2},\frac{1}{2}}_{1,0,\frac{3}{2},\frac{1}{2}} C^{2,0}_{2,0,0,0} C^{\frac{3}{2},\frac{1}{2}}_{2,0,\frac{1}{2},\frac{1}{2}} D^{\frac{1}{2}}_{- \frac{1}{2},\frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{2}_{0,0}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{a_{2}(1320)^{0}} m_{a_{2}(1320)^{0}} - m_{01}^{2} + \left(m_{a_{2}(1320)^{0}}\right)^{2}} \\ \;&+\; \frac{C_{p\gamma (s1/2) \xrightarrow[S=5/2]{L=3} a_{2}(1320)^{0} p; a_{2}(1320)^{0} \xrightarrow[S=0]{L=2} \eta \pi^{0}} \Gamma_{a_{2}(1320)^{0}} m_{a_{2}(1320)^{0}} C^{0,0}_{0,0,0,0} C^{\frac{5}{2},- \frac{1}{2}}_{2,-1,\frac{1}{2},\frac{1}{2}} C^{2,0}_{2,0,0,0} C^{\frac{1}{2},- \frac{1}{2}}_{3,0,\frac{5}{2},- \frac{1}{2}} D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{2}_{-1,0}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{a_{2}(1320)^{0}} m_{a_{2}(1320)^{0}} - m_{01}^{2} + \left(m_{a_{2}(1320)^{0}}\right)^{2}} \\ \;&+\; \frac{C_{p\gamma (s1/2) \xrightarrow[S=5/2]{L=3} a_{2}(1320)^{0} p; a_{2}(1320)^{0} \xrightarrow[S=0]{L=2} \eta \pi^{0}} \Gamma_{a_{2}(1320)^{0}} m_{a_{2}(1320)^{0}} C^{0,0}_{0,0,0,0} C^{2,0}_{2,0,0,0} C^{\frac{5}{2},\frac{1}{2}}_{2,0,\frac{1}{2},\frac{1}{2}} C^{\frac{1}{2},\frac{1}{2}}_{3,0,\frac{5}{2},\frac{1}{2}} D^{\frac{1}{2}}_{- \frac{1}{2},\frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{2}_{0,0}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{a_{2}(1320)^{0}} m_{a_{2}(1320)^{0}} - m_{01}^{2} + \left(m_{a_{2}(1320)^{0}}\right)^{2}} \\ \end{aligned}\end{split}\]

Show code cell source

Hide code cell source

sorted_parameter_defaults = {
    symbol: model.parameter_defaults[symbol]
    for symbol in sorted(model.parameter_defaults, key=str)
}
src = aslatex(sorted_parameter_defaults)
Math(src)

\[\begin{split}\displaystyle \begin{aligned} C_{p\gamma (s1/2) \xrightarrow[S=1/2]{L=1} N(1535)^{+} \eta; N(1535)^{+} \xrightarrow[S=1/2]{L=0} p \pi^{0}} \;&=\; 1+0i \\ C_{p\gamma (s1/2) \xrightarrow[S=1/2]{L=1} N(1535)^{+} \pi^{0}; N(1535)^{+} \xrightarrow[S=1/2]{L=0} \eta p} \;&=\; 1+0i \\ C_{p\gamma (s1/2) \xrightarrow[S=3/2]{L=1} a_{2}(1320)^{0} p; a_{2}(1320)^{0} \xrightarrow[S=0]{L=2} \eta \pi^{0}} \;&=\; 1+0i \\ C_{p\gamma (s1/2) \xrightarrow[S=3/2]{L=2} \Delta(1232)^{+} \eta; \Delta(1232)^{+} \xrightarrow[S=1/2]{L=1} p \pi^{0}} \;&=\; 1+0i \\ C_{p\gamma (s1/2) \xrightarrow[S=5/2]{L=3} a_{2}(1320)^{0} p; a_{2}(1320)^{0} \xrightarrow[S=0]{L=2} \eta \pi^{0}} \;&=\; 1+0i \\ \Gamma_{N(1535)^{+}} \;&=\; 0.15 \\ \Gamma_{\Delta(1232)^{+}} \;&=\; 0.117 \\ \Gamma_{a_{2}(1320)^{0}} \;&=\; 0.107 \\ m_{0} \;&=\; 0.547862 \\ m_{012} \;&=\; 4.101931071854584 \\ m_{1} \;&=\; 0.1349768 \\ m_{2} \;&=\; 0.93827208816 \\ m_{N(1535)^{+}} \;&=\; 1.53 \\ m_{\Delta(1232)^{+}} \;&=\; 1.232 \\ m_{a_{2}(1320)^{0}} \;&=\; 1.3182 \\ \end{aligned}\end{split}\]

Show code cell source

Hide code cell source

Math(aslatex(model.kinematic_variables))

\[\begin{split}\displaystyle \begin{aligned} m_{01} \;&=\; m_{{p}_{01}} \\ m_{02} \;&=\; m_{{p}_{02}} \\ m_{12} \;&=\; m_{{p}_{12}} \\ \phi_{0} \;&=\; \phi\left({p}_{12}\right) \\ \phi^{01}_{0} \;&=\; \phi\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{01}}\right|}{E\left({p}_{01}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{01}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{01}\right)\right) p_{0}\right) \\ \phi^{02}_{0} \;&=\; \phi\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{02}}\right|}{E\left({p}_{02}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{02}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{02}\right)\right) p_{0}\right) \\ \phi_{01} \;&=\; \phi\left({p}_{01}\right) \\ \phi^{12}_{1} \;&=\; \phi\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{12}}\right|}{E\left({p}_{12}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{12}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{12}\right)\right) p_{1}\right) \\ \phi_{02} \;&=\; \phi\left({p}_{02}\right) \\ \theta_{0} \;&=\; \theta\left({p}_{12}\right) \\ \theta^{01}_{0} \;&=\; \theta\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{01}}\right|}{E\left({p}_{01}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{01}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{01}\right)\right) p_{0}\right) \\ \theta^{02}_{0} \;&=\; \theta\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{02}}\right|}{E\left({p}_{02}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{02}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{02}\right)\right) p_{0}\right) \\ \theta_{01} \;&=\; \theta\left({p}_{01}\right) \\ \theta^{12}_{1} \;&=\; \theta\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{12}}\right|}{E\left({p}_{12}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{12}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{12}\right)\right) p_{1}\right) \\ \theta_{02} \;&=\; \theta\left({p}_{02}\right) \\ \end{aligned}\end{split}\]

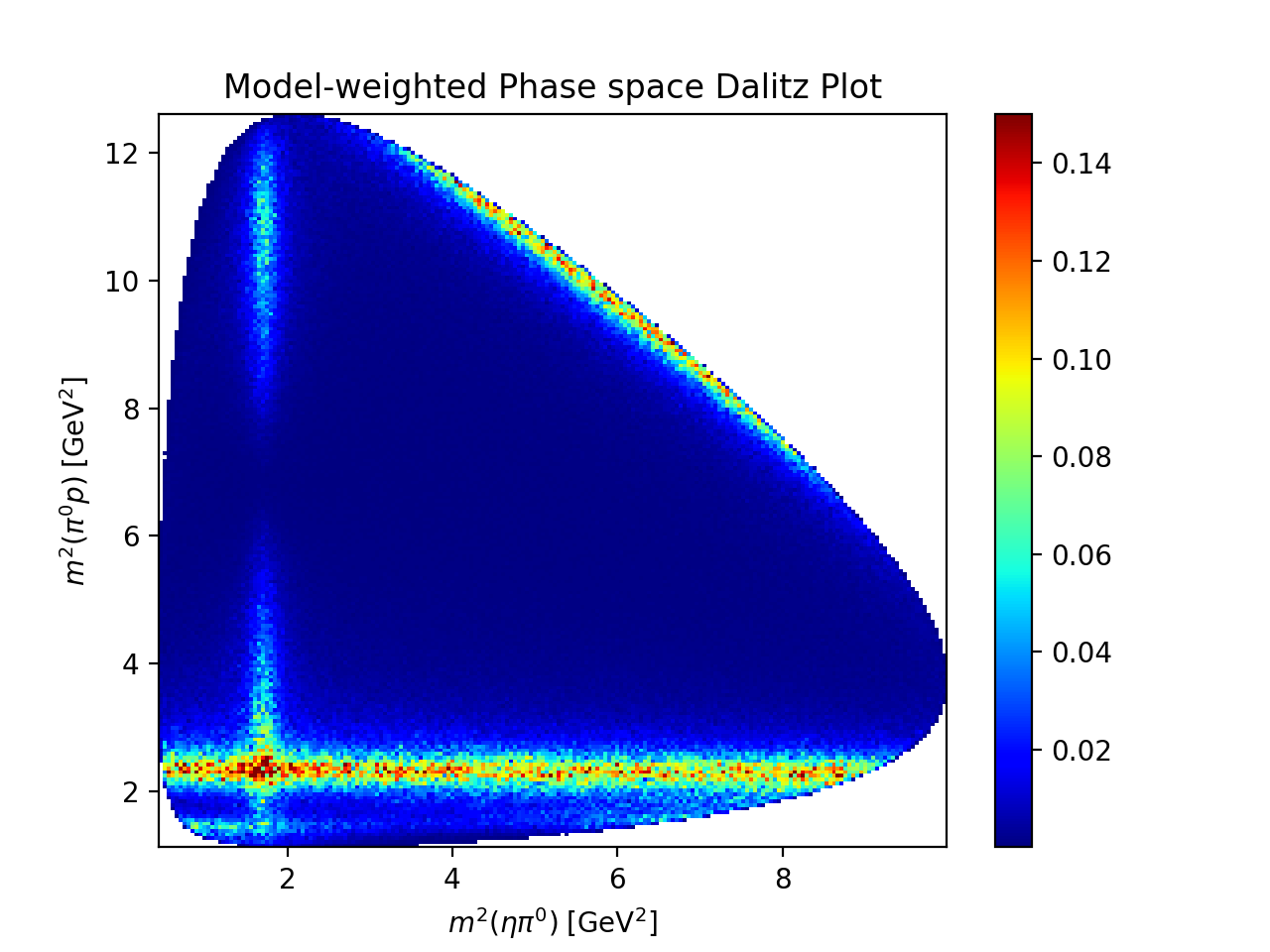
Visualization

unfolded_expression = model.expression.doit()
intensity_func = create_parametrized_function(
    expression=unfolded_expression,
    parameters=model.parameter_defaults,
    backend="jax",
)

phsp_event = 500_000
rng = TFUniformRealNumberGenerator(seed=0)
phsp_generator = TFPhaseSpaceGenerator(
    initial_state_mass=reaction.initial_state[-1].mass,
    final_state_masses={i: p.mass for i, p in reaction.final_state.items()},
)
phsp_momenta = phsp_generator.generate(phsp_event, rng)

Show code cell output

Hide code cell output

WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1760541835.503451    3599 device_compiler.h:196] Compiled cluster using XLA!  This line is logged at most once for the lifetime of the process.

helicity_transformer = SympyDataTransformer.from_sympy(
    model.kinematic_variables,
    backend="jax",
)
phsp = helicity_transformer(phsp_momenta)

Collect resonances for each subsystem

Hide code cell source

resonances = defaultdict(set)
for transition in reaction.transitions:
    topology = transition.topology
    top_decay_products = topology.get_edge_ids_outgoing_from_node(0)
    (resonance_id, resonance), *_ = transition.intermediate_states.items()
    recoil_id, *_ = top_decay_products - {resonance_id}
    resonances[recoil_id].add(resonance.particle)
resonances = {k: sorted(v, key=lambda p: p.mass) for k, v in resonances.items()}
{k: [p.name for p in v] for k, v in resonances.items()}

{0: ['Delta(1232)+', 'N(1535)+'], 1: ['N(1535)+'], 2: ['a(2)(1320)0']}

Design slider UI

Hide code cell source

sliders = {}
categorized_sliders_m = defaultdict(list)
categorized_sliders_gamma = defaultdict(list)
categorized_cphi_pair = defaultdict(list)

for symbol, value in model.parameter_defaults.items():
    if symbol.name.startswith(R"\Gamma_{"):
        slider = w.FloatSlider(
            description=Rf"\({sp.latex(symbol)}\)",
            min=0.0,
            max=1.0,
            step=0.01,
            value=value,
            continuous_update=False,
        )
        sliders[symbol.name] = slider
        if symbol.name.startswith(R"\Gamma_{N"):
            categorized_sliders_gamma[0].append(slider)
        elif symbol.name.startswith(R"\Gamma_{\D"):
            categorized_sliders_gamma[1].append(slider)
        elif symbol.name.startswith(R"\Gamma_{a"):
            categorized_sliders_gamma[2].append(slider)

    if symbol.name.startswith("m_{"):
        slider = w.FloatSlider(
            description=Rf"\({sp.latex(symbol)}\)",
            min=0.63,
            max=4,
            step=0.01,
            value=value,
            continuous_update=False,
        )
        sliders[symbol.name] = slider
        if symbol.name.startswith("m_{N"):
            categorized_sliders_m[0].append(slider)
        elif symbol.name.startswith(R"m_{\D"):
            categorized_sliders_m[1].append(slider)
        elif symbol.name.startswith("m_{a"):
            categorized_sliders_m[2].append(slider)

    if symbol.name.startswith("C_{"):
        c_latex = sp.latex(symbol)
        phi_latex = c_latex.replace("C", R"\phi", 1)

        slider_c = w.FloatSlider(
            description=Rf"\({c_latex}\)",
            min=0,
            max=10,
            step=0.01,
            value=abs(value),
            continuous_update=False,
        )
        slider_phi = w.FloatSlider(
            description=Rf"\({phi_latex}\)",
            min=-np.pi,
            max=+np.pi,
            step=0.01,
            value=np.angle(value),
            continuous_update=False,
        )

        sliders[symbol.name] = slider_c
        sliders[symbol.name.replace("C", "phi", 1)] = slider_phi

        cphi_hbox = w.HBox([slider_c, slider_phi])
        if R"\D" in symbol.name:
            categorized_cphi_pair[1].append(cphi_hbox)
        elif "N" in symbol.name:
            categorized_cphi_pair[0].append(cphi_hbox)
        elif "a" in symbol.name:
            categorized_cphi_pair[2].append(cphi_hbox)

tab_contents = []
resonances_name = ["N*", "Δ*", "a₂*"]
for i in range(len(resonances_name)):
    tab_content = w.VBox([
        w.HBox(categorized_sliders_m[i] + categorized_sliders_gamma[i]),
        w.VBox(categorized_cphi_pair[i]),
    ])
    tab_contents.append(tab_content)
UI = w.Tab(tab_contents, titles=resonances_name)

Show code cell source

Hide code cell source

def insert_phi(parameters: dict) -> dict:
    updated_parameters = {}
    for key, value in parameters.items():
        if key.startswith("phi_"):
            continue
        if key.startswith("C_"):
            phi_key = key.replace("C_", "phi_")
            if phi_key in parameters:
                phi = parameters[phi_key]
                value *= np.exp(1j * phi)  # noqa:PLW2901
        updated_parameters[key] = value
    return updated_parameters

Show code cell source

Hide code cell source

%matplotlib widget
%config InlineBackend.figure_formats = ['png']
fig_2d, ax_2d = plt.subplots(dpi=200)
ax_2d.set_title("Model-weighted Phase space Dalitz Plot")
ax_2d.set_xlabel(R"$m^2(\eta \pi^0)\;\left[\mathrm{GeV}^2\right]$")
ax_2d.set_ylabel(R"$m^2(\pi^0 p)\;\left[\mathrm{GeV}^2\right]$")

mesh = None


def update_histogram(**parameters):
    global mesh
    parameters = insert_phi(parameters)
    intensity_func.update_parameters(parameters)
    intensity_weights = intensity_func(phsp)
    bin_values, xedges, yedges = jnp.histogram2d(
        phsp["m_01"].real ** 2,
        phsp["m_12"].real ** 2,
        bins=200,
        weights=intensity_weights,
        density=True,
    )
    bin_values = jnp.where(bin_values < 1e-6, jnp.nan, bin_values)
    x, y = jnp.meshgrid(xedges[:-1], yedges[:-1])
    if mesh is None:
        mesh = ax_2d.pcolormesh(x, y, bin_values.T, cmap="jet", vmax=0.15)
    else:
        mesh.set_array(bin_values.T)
    fig_2d.canvas.draw_idle()


interactive_plot = w.interactive_output(update_histogram, sliders)
fig_2d.tight_layout()
fig_2d.colorbar(mesh, ax=ax_2d)

if STATIC_PAGE:
    filename = "dalitz-plot-auto.png"
    fig_2d.savefig(filename)
    plt.close(fig_2d)
    display(UI, Image(filename))
else:
    display(UI, interactive_plot)

Show code cell source

Hide code cell source

%matplotlib widget
%config InlineBackend.figure_formats = ['svg']

fig, axes = plt.subplots(figsize=(11, 3.5), ncols=3, sharey=True)
fig.canvas.toolbar_visible = False
fig.canvas.header_visible = False
fig.canvas.footer_visible = False
ax1, ax2, ax3 = axes

for recoil_id, ax in enumerate(axes):
    decay_products = sorted({0, 1, 2} - {recoil_id})
    product_latex = " ".join([reaction.final_state[i].latex for i in decay_products])
    ax.set_xlabel(f"$m({product_latex})$ [GeV]")

LINES = 3 * [None]
RESONANCE_LINES = defaultdict(dict)


def update_plot(**parameters):
    parameters = insert_phi(parameters)
    intensity_func.update_parameters(parameters)
    intensities = intensity_func(phsp)
    max_value = 0
    resonance_colors: dict[Particle, int] = {}
    color_id = 0
    for recoil_id, ax in enumerate(axes):
        decay_products = sorted({0, 1, 2} - {recoil_id})
        key = f"m_{''.join(str(i) for i in decay_products)}"
        bin_values, bin_edges = jax.numpy.histogram(
            phsp[key].real,
            bins=120,
            density=True,
            weights=intensities,
        )
        max_value = max(max_value, bin_values.max())

        if LINES[recoil_id] is None:
            LINES[recoil_id] = ax.step(bin_edges[:-1], bin_values, alpha=0.5)[0]
        else:
            LINES[recoil_id].set_ydata(bin_values)

        for resonance in resonances[recoil_id]:
            key = f"m_{{{resonance.latex}}}"
            val = parameters.get(key, resonance.mass)
            resonance_line = RESONANCE_LINES[recoil_id].get(resonance.name)
            if resonance_line is None:
                RESONANCE_LINES[recoil_id][resonance.name] = ax.axvline(
                    val,
                    c=f"C{resonance_colors.get(resonance, color_id)}",
                    ls="dotted",
                    label=resonance.name,
                )
            else:
                resonance_line.set_xdata([val, val])
            if resonance not in resonance_colors:
                resonance_colors[resonance] = color_id
                color_id += 1

    for ax in axes:
        ax.set_ylim(0, max_value * 1.1)


interactive_plot = w.interactive_output(update_plot, sliders)
for ax in axes:
    ax.legend(fontsize="small")
fig.tight_layout()

if STATIC_PAGE:
    filename = "1d-histograms-auto.svg"
    fig.savefig(filename)
    plt.close(fig)
    display(UI, SVG(filename))
else:
    display(UI, interactive_plot)