Amplitude model with ampform

PWA study on \(p \gamma \to \Lambda K^+ \pi^0\). We formulate the helicity amplitude model symbolically using AmpForm here.

Import Python libraries Hide code cell source

import logging
import os
import warnings
from collections import defaultdict
from fractions import Fraction
from textwrap import dedent

import ampform
import graphviz
import ipywidgets as w
import jax
import jax.numpy as jnp
import matplotlib.pyplot as plt
import numpy as np
import qrules
import sympy as sp
from ampform.dynamics.builder import RelativisticBreitWignerBuilder
from ampform.io import aslatex, improve_latex_rendering
from IPython.display import SVG, Image, Markdown, Math, display
from qrules.particle import Particle, Spin, create_particle, load_pdg
from tensorwaves.data import (
    SympyDataTransformer,
    TFPhaseSpaceGenerator,
    TFUniformRealNumberGenerator,
)
from tensorwaves.function.sympy import create_parametrized_function

STATIC_PAGE = "EXECUTE_NB" in os.environ

os.environ["TF_CPP_MIN_LOG_LEVEL"] = "3"
logging.disable(logging.WARNING)
warnings.filterwarnings("ignore")

improve_latex_rendering()
particle_db = load_pdg()

Decay definition

Particle definitions

Show code cell source Hide code cell source

def generate_markdown_table(particles: list[str]):
    src = dedent(r"""
    | Particle | Name | PID | $J^{PC} (I^G)$ | $I_3$ | $M$ | $\Gamma$ | $Q$ | $S$ | $B$ |
    | :------- |------|-----|----------------|-------|-----|----------|-----|-----|-----|
    """)
    for name in particles:
        p = particle_db[name]
        src += f"| ${p.latex}$ | `{p.name}` | {p.pid} | {jpc_ig(p)} | {i_3(p)} |  {p.mass:.3g}| {p.width:g} | {p.charge} |{p.strangeness} | {p.baryon_number}|\n"
    return src


def jpc_ig(particle: Particle) -> str:
    j = format_fraction(particle.spin)
    p = format_parity(particle.parity)
    c = format_parity(particle.c_parity)
    if particle.isospin is None:
        return f"${j}^{{{p}{c}}}$"
    i = format_fraction(particle.isospin.magnitude)
    g = format_parity(particle.g_parity)
    return rf"${j}^{{{p}{c}}} \; ({i}^{{{g}}})$"


def i_3(particle: Particle) -> str:
    if particle.isospin is None:
        return "N/A"
    return f"${format_fraction(particle.isospin.projection)}$"


def format_fraction(value: float) -> str:
    value = Fraction(value)
    if value.denominator == 1:
        return str(value.numerator)
    return rf"\frac{{{value.numerator}}}{{{value.denominator}}}"


def format_parity(parity: int | None) -> str:
    if parity is None:
        return " "
    if parity == -1:
        return "-"
    if parity == 1:
        return "+"
    raise NotImplementedError


particles = ["Lambda", "K+", "pi0", "gamma", "p"]
src = generate_markdown_table(particles)
Markdown(src)

Particle	Name	PID	\(J^{PC} (I^G)\)	\(I_3\)	\(M\)	\(\Gamma\)	\(Q\)	\(S\)	\(B\)
\(\Lambda\)	Lambda	3122	\(\frac{1}{2}^{+ } \; (0^{ })\)	\(0\)	1.12	2.515e-15	0	-1	1
\(K^{+}\)	K+	321	\(0^{- } \; (\frac{1}{2}^{ })\)	\(\frac{1}{2}\)	0.494	5.317e-17	1	1	0
\(\pi^{0}\)	pi0	111	\(0^{-+} \; (1^{-})\)	\(0\)	0.135	7.81e-09	0	0	0
\(\gamma\)	gamma	22	\(1^{--}\)	N/A	0	0	0	0	0
\(p\)	p	2212	\(\frac{1}{2}^{+ } \; (\frac{1}{2}^{ })\)	\(\frac{1}{2}\)	0.938	0	1	0	1

In the table above, PID is the PDG ID from PDG particle numbering scheme, \(J\) is the spin, \(P\) is the parity, \(C\) is the C parity, \(I\) is the isospin (magnitude), \(G\) is the G parity. \(I_3\) is the isospin projection (or the 3rd component), \(M\) is the mass, \(\Gamma\) is the width, \(Q\) is the charge, \(S\) is the strangeness number, and \(B\) is the baryon number.

Initial state definition

Mass for \(p \gamma\) system

E_lab_gamma = 8.5
m_proton = 0.938
m_0 = np.sqrt(2 * E_lab_gamma * m_proton + m_proton**2)
m_eta = 0.548
m_pi = 0.135
m_0

np.float64(4.101931740046389)

Add custom particle \(p \gamma\)

pgamma1 = Particle(
    name="pgamma1",
    latex=r"p\gamma (s1/2)",
    spin=0.5,
    mass=m_0,
    charge=1,
    isospin=Spin(1 / 2, +1 / 2),
    baryon_number=1,
    parity=-1,
    pid=99990,
)
pgamma2 = create_particle(
    template_particle=pgamma1,
    name="pgamma2",
    latex=R"p\gamma (s3/2)",
    spin=1.5,
    pid=pgamma1.pid + 1,
)
particle_db.update([pgamma1, pgamma2])

Generate transitions

For simplicity, we use the initial state \(p \gamma\) (with spin-\(\frac{1}{2}\)), and set the allowed interaction type to be strong only, the formalism is selected to be helicity formalism instead of canonical.

See also

Helicity versus canonical

reaction = qrules.generate_transitions(
    initial_state=("pgamma1"),
    final_state=["Lambda", "K+", "pi0"],
    allowed_interaction_types=["strong"],
    formalism="helicity",
    particle_db=particle_db,
    max_angular_momentum=4,
    max_spin_magnitude=4,
    mass_conservation_factor=0,
)

Show code cell source Hide code cell source

dot = qrules.io.asdot(reaction, collapse_graphs=True)
graphviz.Source(dot)

Formulate amplitude model

model_builder = ampform.get_builder(reaction)
model_builder.config.scalar_initial_state_mass = True
model_builder.config.stable_final_state_ids = 0, 1, 2
bw_builder = RelativisticBreitWignerBuilder(
    energy_dependent_width=False,
    form_factor=False,
)
for name in reaction.get_intermediate_particles().names:
    model_builder.dynamics.assign(name, bw_builder)
model = model_builder.formulate()

model.intensity

\[\displaystyle \sum_{m_{A}=-1/2}^{1/2} \sum_{m_{0}=-1/2}^{1/2} \sum_{m_{1}=0} \sum_{m_{2}=0}{\left|{A^{01}_{m_{A}, m_{0}, m_{1}, m_{2}} + A^{02}_{m_{A}, m_{0}, m_{1}, m_{2}} + A^{12}_{m_{A}, m_{0}, m_{1}, m_{2}}}\right|^{2}}\]

The first term in the amplitude model:

Show code cell source Hide code cell source

(symbol, expr), *_ = model.amplitudes.items()
Math(aslatex({symbol: expr}, terms_per_line=1))

\[\begin{split}\displaystyle \begin{array}{rcl} A^{01}_{- \frac{1}{2}, - \frac{1}{2}, 0, 0} &=& - \frac{C_{p\gamma (s1/2) \to N(1650)^{+}_{+1/2} \pi^{0}_{0}; N(1650)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1650)^{+}} m_{N(1650)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1650)^{+}} m_{N(1650)^{+}} - m_{01}^{2} + \left(m_{N(1650)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1650)^{+}_{+1/2} \pi^{0}_{0}; N(1650)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1650)^{+}} m_{N(1650)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},\frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{1}{2}}_{\frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1650)^{+}} m_{N(1650)^{+}} - m_{01}^{2} + \left(m_{N(1650)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1675)^{+}_{+1/2} \pi^{0}_{0}; N(1675)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1675)^{+}} m_{N(1675)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{5}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1675)^{+}} m_{N(1675)^{+}} - m_{01}^{2} + \left(m_{N(1675)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1675)^{+}_{+1/2} \pi^{0}_{0}; N(1675)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1675)^{+}} m_{N(1675)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},\frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{5}{2}}_{\frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1675)^{+}} m_{N(1675)^{+}} - m_{01}^{2} + \left(m_{N(1675)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1680)^{+}_{+1/2} \pi^{0}_{0}; N(1680)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1680)^{+}} m_{N(1680)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{5}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1680)^{+}} m_{N(1680)^{+}} - m_{01}^{2} + \left(m_{N(1680)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1680)^{+}_{+1/2} \pi^{0}_{0}; N(1680)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1680)^{+}} m_{N(1680)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},\frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{5}{2}}_{\frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1680)^{+}} m_{N(1680)^{+}} - m_{01}^{2} + \left(m_{N(1680)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1700)^{+}_{+1/2} \pi^{0}_{0}; N(1700)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1700)^{+}} m_{N(1700)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{3}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1700)^{+}} m_{N(1700)^{+}} - m_{01}^{2} + \left(m_{N(1700)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1700)^{+}_{+1/2} \pi^{0}_{0}; N(1700)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1700)^{+}} m_{N(1700)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},\frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{3}{2}}_{\frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1700)^{+}} m_{N(1700)^{+}} - m_{01}^{2} + \left(m_{N(1700)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1710)^{+}_{+1/2} \pi^{0}_{0}; N(1710)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1710)^{+}} m_{N(1710)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1710)^{+}} m_{N(1710)^{+}} - m_{01}^{2} + \left(m_{N(1710)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1710)^{+}_{+1/2} \pi^{0}_{0}; N(1710)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1710)^{+}} m_{N(1710)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},\frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{1}{2}}_{\frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1710)^{+}} m_{N(1710)^{+}} - m_{01}^{2} + \left(m_{N(1710)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1720)^{+}_{+1/2} \pi^{0}_{0}; N(1720)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1720)^{+}} m_{N(1720)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{3}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1720)^{+}} m_{N(1720)^{+}} - m_{01}^{2} + \left(m_{N(1720)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(1720)^{+}_{+1/2} \pi^{0}_{0}; N(1720)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(1720)^{+}} m_{N(1720)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},\frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{3}{2}}_{\frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(1720)^{+}} m_{N(1720)^{+}} - m_{01}^{2} + \left(m_{N(1720)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(2190)^{+}_{+1/2} \pi^{0}_{0}; N(2190)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(2190)^{+}} m_{N(2190)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{7}{2}}_{- \frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(2190)^{+}} m_{N(2190)^{+}} - m_{01}^{2} + \left(m_{N(2190)^{+}}\right)^{2}} \\ &+& - \frac{C_{p\gamma (s1/2) \to N(2190)^{+}_{+1/2} \pi^{0}_{0}; N(2190)^{+} \to K^{+}_{0} \Lambda_{+1/2}} \Gamma_{N(2190)^{+}} m_{N(2190)^{+}} D^{\frac{1}{2}}_{- \frac{1}{2},\frac{1}{2}}\left(- \phi_{01},\theta_{01},0\right) D^{\frac{7}{2}}_{\frac{1}{2},- \frac{1}{2}}\left(- \phi^{01}_{0},\theta^{01}_{0},0\right)}{- i \Gamma_{N(2190)^{+}} m_{N(2190)^{+}} - m_{01}^{2} + \left(m_{N(2190)^{+}}\right)^{2}} \\ \end{array}\end{split}\]

Model parameters Hide code cell source

Math(aslatex(model.parameter_defaults))

\[\begin{split}\displaystyle \begin{array}{rcl} m_{K_{0}^{*}(700)^{+}} &=& 0.845 \\ \Gamma_{K_{0}^{*}(700)^{+}} &=& 0.468 \\ C_{p\gamma (s1/2) \to {K_{0}^{*}(700)^{+}}_{0} \Lambda_{+1/2}; K_{0}^{*}(700)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{K^{*}(892)^{+}} &=& 0.89167 \\ \Gamma_{K^{*}(892)^{+}} &=& 0.0514 \\ C_{p\gamma (s1/2) \to K^{*}(892)^{+}_{+1} \Lambda_{+1/2}; K^{*}(892)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ C_{p\gamma (s1/2) \to K^{*}(892)^{+}_{0} \Lambda_{+1/2}; K^{*}(892)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{K^{*}(1410)^{+}} &=& 1.414 \\ \Gamma_{K^{*}(1410)^{+}} &=& 0.232 \\ C_{p\gamma (s1/2) \to K^{*}(1410)^{+}_{+1} \Lambda_{+1/2}; K^{*}(1410)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ C_{p\gamma (s1/2) \to K^{*}(1410)^{+}_{0} \Lambda_{+1/2}; K^{*}(1410)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{K_{2}^{*}(1430)^{+}} &=& 1.4273 \\ \Gamma_{K_{2}^{*}(1430)^{+}} &=& 0.1 \\ C_{p\gamma (s1/2) \to {K_{2}^{*}(1430)^{+}}_{+1} \Lambda_{+1/2}; K_{2}^{*}(1430)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ C_{p\gamma (s1/2) \to {K_{2}^{*}(1430)^{+}}_{0} \Lambda_{+1/2}; K_{2}^{*}(1430)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{K_{0}^{*}(1430)^{+}} &=& 1.43 \\ \Gamma_{K_{0}^{*}(1430)^{+}} &=& 0.27 \\ C_{p\gamma (s1/2) \to {K_{0}^{*}(1430)^{+}}_{0} \Lambda_{+1/2}; K_{0}^{*}(1430)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{K^{*}(1680)^{+}} &=& 1.718 \\ \Gamma_{K^{*}(1680)^{+}} &=& 0.32 \\ C_{p\gamma (s1/2) \to K^{*}(1680)^{+}_{+1} \Lambda_{+1/2}; K^{*}(1680)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ C_{p\gamma (s1/2) \to K^{*}(1680)^{+}_{0} \Lambda_{+1/2}; K^{*}(1680)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{K_{3}^{*}(1780)^{+}} &=& 1.779 \\ \Gamma_{K_{3}^{*}(1780)^{+}} &=& 0.161 \\ C_{p\gamma (s1/2) \to {K_{3}^{*}(1780)^{+}}_{+1} \Lambda_{+1/2}; K_{3}^{*}(1780)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ C_{p\gamma (s1/2) \to {K_{3}^{*}(1780)^{+}}_{0} \Lambda_{+1/2}; K_{3}^{*}(1780)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{K_{0}^{*}(1950)^{+}} &=& 1.957 \\ \Gamma_{K_{0}^{*}(1950)^{+}} &=& 0.17 \\ C_{p\gamma (s1/2) \to {K_{0}^{*}(1950)^{+}}_{0} \Lambda_{+1/2}; K_{0}^{*}(1950)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{K_{2}^{*}(1980)^{+}} &=& 1.99 \\ \Gamma_{K_{2}^{*}(1980)^{+}} &=& 0.348 \\ C_{p\gamma (s1/2) \to {K_{2}^{*}(1980)^{+}}_{+1} \Lambda_{+1/2}; K_{2}^{*}(1980)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ C_{p\gamma (s1/2) \to {K_{2}^{*}(1980)^{+}}_{0} \Lambda_{+1/2}; K_{2}^{*}(1980)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{K_{4}^{*}(2045)^{+}} &=& 2.048 \\ \Gamma_{K_{4}^{*}(2045)^{+}} &=& 0.199 \\ C_{p\gamma (s1/2) \to {K_{4}^{*}(2045)^{+}}_{+1} \Lambda_{+1/2}; K_{4}^{*}(2045)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ C_{p\gamma (s1/2) \to {K_{4}^{*}(2045)^{+}}_{0} \Lambda_{+1/2}; K_{4}^{*}(2045)^{+} \to K^{+}_{0} \pi^{0}_{0}} &=& 1+0i \\ m_{\Sigma(1385)^{0}} &=& 1.3837000000000002 \\ \Gamma_{\Sigma(1385)^{0}} &=& 0.036 \\ C_{p\gamma (s1/2) \to K^{+}_{0} \Sigma(1385)^{0}_{+1/2}; \Sigma(1385)^{0} \to \Lambda_{+1/2} \pi^{0}_{0}} &=& 1+0i \\ m_{\Sigma(1660)^{0}} &=& 1.66 \\ \Gamma_{\Sigma(1660)^{0}} &=& 0.2 \\ C_{p\gamma (s1/2) \to K^{+}_{0} \Sigma(1660)^{0}_{+1/2}; \Sigma(1660)^{0} \to \Lambda_{+1/2} \pi^{0}_{0}} &=& 1+0i \\ m_{\Sigma(1670)^{0}} &=& 1.675 \\ \Gamma_{\Sigma(1670)^{0}} &=& 0.07 \\ C_{p\gamma (s1/2) \to K^{+}_{0} \Sigma(1670)^{0}_{+1/2}; \Sigma(1670)^{0} \to \Lambda_{+1/2} \pi^{0}_{0}} &=& 1+0i \\ m_{\Sigma(1750)^{0}} &=& 1.75 \\ \Gamma_{\Sigma(1750)^{0}} &=& 0.15 \\ C_{p\gamma (s1/2) \to K^{+}_{0} \Sigma(1750)^{0}_{+1/2}; \Sigma(1750)^{0} \to \Lambda_{+1/2} \pi^{0}_{0}} &=& 1+0i \\ m_{\Sigma(1775)^{0}} &=& 1.775 \\ \Gamma_{\Sigma(1775)^{0}} &=& 0.12 \\ C_{p\gamma (s1/2) \to K^{+}_{0} \Sigma(1775)^{0}_{+1/2}; \Sigma(1775)^{0} \to \Lambda_{+1/2} \pi^{0}_{0}} &=& 1+0i \\ m_{\Sigma(1940)^{0}} &=& 1.91 \\ \Gamma_{\Sigma(1940)^{0}} &=& 0.22 \\ C_{p\gamma (s1/2) \to K^{+}_{0} \Sigma(1940)^{0}_{+1/2}; \Sigma(1940)^{0} \to \Lambda_{+1/2} \pi^{0}_{0}} &=& 1+0i \\ m_{\Sigma(1915)^{0}} &=& 1.915 \\ \Gamma_{\Sigma(1915)^{0}} &=& 0.12 \\ C_{p\gamma (s1/2) \to K^{+}_{0} \Sigma(1915)^{0}_{+1/2}; \Sigma(1915)^{0} \to \Lambda_{+1/2} \pi^{0}_{0}} &=& 1+0i \\ m_{\Sigma(2030)^{0}} &=& 2.03 \\ \Gamma_{\Sigma(2030)^{0}} &=& 0.18 \\ C_{p\gamma (s1/2) \to K^{+}_{0} \Sigma(2030)^{0}_{+1/2}; \Sigma(2030)^{0} \to \Lambda_{+1/2} \pi^{0}_{0}} &=& 1+0i \\ m_{N(1650)^{+}} &=& 1.65 \\ \Gamma_{N(1650)^{+}} &=& 0.125 \\ C_{p\gamma (s1/2) \to N(1650)^{+}_{+1/2} \pi^{0}_{0}; N(1650)^{+} \to K^{+}_{0} \Lambda_{+1/2}} &=& 1+0i \\ m_{N(1675)^{+}} &=& 1.675 \\ \Gamma_{N(1675)^{+}} &=& 0.145 \\ C_{p\gamma (s1/2) \to N(1675)^{+}_{+1/2} \pi^{0}_{0}; N(1675)^{+} \to K^{+}_{0} \Lambda_{+1/2}} &=& 1+0i \\ m_{N(1680)^{+}} &=& 1.685 \\ \Gamma_{N(1680)^{+}} &=& 0.12 \\ C_{p\gamma (s1/2) \to N(1680)^{+}_{+1/2} \pi^{0}_{0}; N(1680)^{+} \to K^{+}_{0} \Lambda_{+1/2}} &=& 1+0i \\ m_{N(1710)^{+}} &=& 1.71 \\ \Gamma_{N(1710)^{+}} &=& 0.14 \\ C_{p\gamma (s1/2) \to N(1710)^{+}_{+1/2} \pi^{0}_{0}; N(1710)^{+} \to K^{+}_{0} \Lambda_{+1/2}} &=& 1+0i \\ m_{N(1700)^{+}} &=& 1.72 \\ \Gamma_{N(1700)^{+}} &=& 0.2 \\ C_{p\gamma (s1/2) \to N(1700)^{+}_{+1/2} \pi^{0}_{0}; N(1700)^{+} \to K^{+}_{0} \Lambda_{+1/2}} &=& 1+0i \\ m_{N(1720)^{+}} &=& 1.72 \\ \Gamma_{N(1720)^{+}} &=& 0.25 \\ C_{p\gamma (s1/2) \to N(1720)^{+}_{+1/2} \pi^{0}_{0}; N(1720)^{+} \to K^{+}_{0} \Lambda_{+1/2}} &=& 1+0i \\ m_{N(2190)^{+}} &=& 2.18 \\ \Gamma_{N(2190)^{+}} &=& 0.4 \\ C_{p\gamma (s1/2) \to N(2190)^{+}_{+1/2} \pi^{0}_{0}; N(2190)^{+} \to K^{+}_{0} \Lambda_{+1/2}} &=& 1+0i \\ m_{0} &=& 1.115683 \\ m_{1} &=& 0.49367700000000003 \\ m_{2} &=& 0.1349768 \\ m_{012} &=& 4.101931740046389 \\ \end{array}\end{split}\]

Kinematic variable definitions Hide code cell source

Math(aslatex(model.kinematic_variables))

\[\begin{split}\displaystyle \begin{array}{rcl} m_{01} &=& m_{{p}_{01}} \\ m_{02} &=& m_{{p}_{02}} \\ m_{12} &=& m_{{p}_{12}} \\ \phi_{0} &=& \phi\left({p}_{12}\right) \\ \phi^{01}_{0} &=& \phi\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{01}}\right|}{E\left({p}_{01}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{01}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{01}\right)\right) p_{0}\right) \\ \phi^{02}_{0} &=& \phi\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{02}}\right|}{E\left({p}_{02}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{02}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{02}\right)\right) p_{0}\right) \\ \phi_{01} &=& \phi\left({p}_{01}\right) \\ \phi^{12}_{1} &=& \phi\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{12}}\right|}{E\left({p}_{12}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{12}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{12}\right)\right) p_{1}\right) \\ \phi_{02} &=& \phi\left({p}_{02}\right) \\ \theta_{0} &=& \theta\left({p}_{12}\right) \\ \theta^{01}_{0} &=& \theta\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{01}}\right|}{E\left({p}_{01}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{01}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{01}\right)\right) p_{0}\right) \\ \theta^{02}_{0} &=& \theta\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{02}}\right|}{E\left({p}_{02}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{02}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{02}\right)\right) p_{0}\right) \\ \theta_{01} &=& \theta\left({p}_{01}\right) \\ \theta^{12}_{1} &=& \theta\left(\boldsymbol{B_z}\left(\frac{\left|\vec{{p}_{12}}\right|}{E\left({p}_{12}\right)}\right) \boldsymbol{R_y}\left(- \theta\left({p}_{12}\right)\right) \boldsymbol{R_z}\left(- \phi\left({p}_{12}\right)\right) p_{1}\right) \\ \theta_{02} &=& \theta\left({p}_{02}\right) \\ \end{array}\end{split}\]

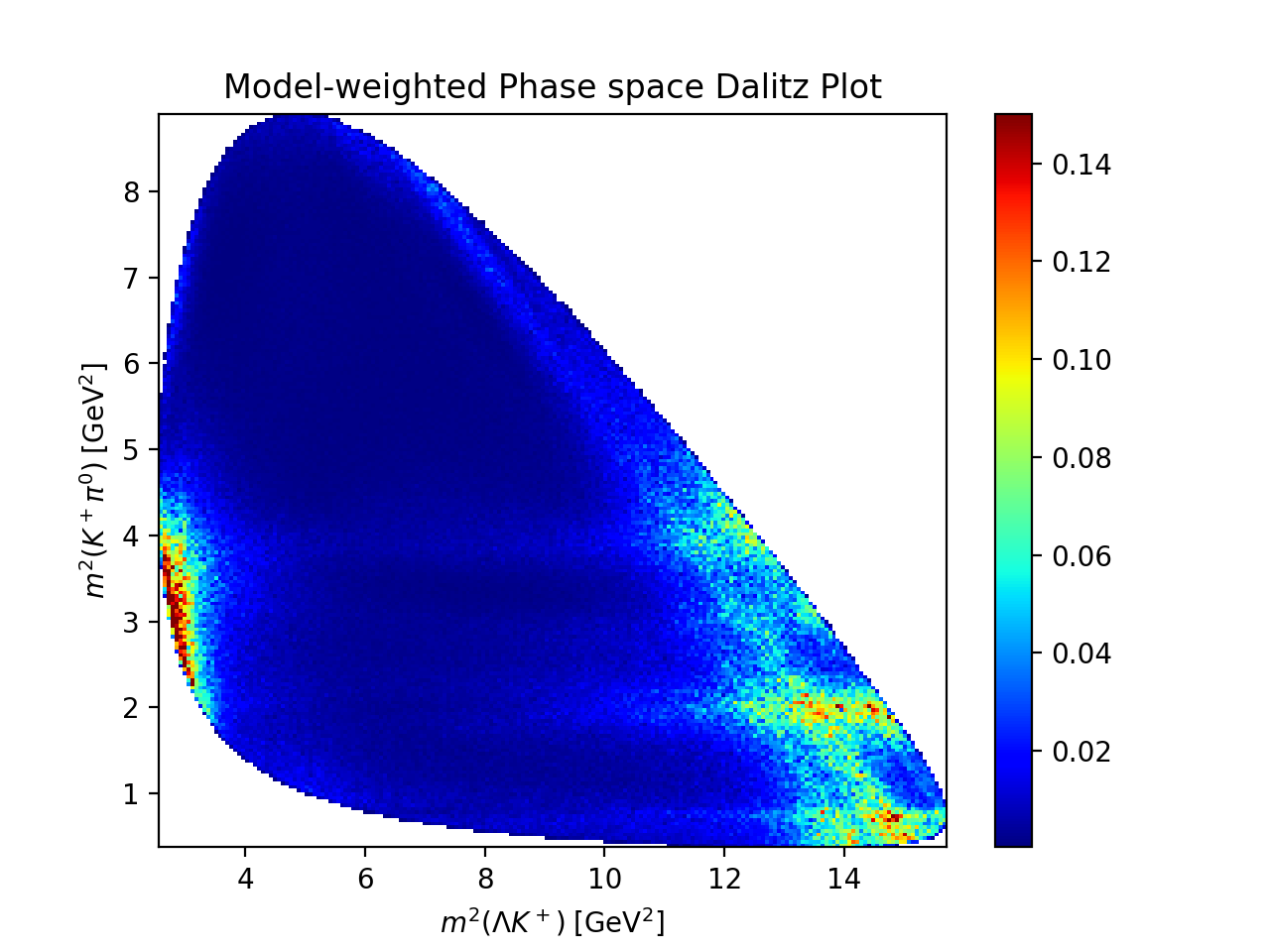
Visualization

unfolded_expression = model.expression.doit()
intensity_func = create_parametrized_function(
    expression=unfolded_expression,
    parameters=model.parameter_defaults,
    backend="jax",
)

phsp_event = 500_000
rng = TFUniformRealNumberGenerator(seed=0)
phsp_generator = TFPhaseSpaceGenerator(
    initial_state_mass=reaction.initial_state[-1].mass,
    final_state_masses={i: p.mass for i, p in reaction.final_state.items()},
)
phsp_momenta = phsp_generator.generate(phsp_event, rng)

helicity_transformer = SympyDataTransformer.from_sympy(
    model.kinematic_variables,
    backend="jax",
)
phsp = helicity_transformer(phsp_momenta)

Show code cell source Hide code cell source

resonances = defaultdict(set)
for transition in reaction.transitions:
    topology = transition.topology
    top_decay_products = topology.get_edge_ids_outgoing_from_node(0)
    (resonance_id, resonance), *_ = transition.intermediate_states.items()
    recoil_id, *_ = top_decay_products - {resonance_id}
    resonances[recoil_id].add(resonance.particle)
resonances = {k: sorted(v, key=lambda p: p.mass) for k, v in resonances.items()}
{k: [p.name for p in v] for k, v in resonances.items()}

Show code cell output Hide code cell output

{0: ['K(0)*(700)+',
  'K*(892)+',
  'K*(1410)+',
  'K(2)*(1430)+',
  'K(0)*(1430)+',
  'K*(1680)+',
  'K(3)*(1780)+',
  'K(0)*(1950)+',
  'K(2)*(1980)+',
  'K(4)*(2045)+'],
 1: ['Sigma(1385)0',
  'Sigma(1660)0',
  'Sigma(1670)0',
  'Sigma(1750)0',
  'Sigma(1775)0',
  'Sigma(1910)0',
  'Sigma(1915)0',
  'Sigma(2030)0'],
 2: ['N(1650)+',
  'N(1675)+',
  'N(1680)+',
  'N(1710)+',
  'N(1720)+',
  'N(1700)+',
  'N(2190)+']}

Design slider UI Hide code cell source

sliders = {}
categorized_sliders_m = defaultdict(list)
categorized_sliders_gamma = defaultdict(list)
categorized_cphi_pair = defaultdict(list)

for symbol, value in model.parameter_defaults.items():
    if symbol.name.startswith(R"\Gamma_{"):
        slider = w.FloatSlider(
            description=Rf"\({sp.latex(symbol)}\)",
            min=0.0,
            max=1.0,
            step=0.01,
            value=value,
            continuous_update=False,
        )
        sliders[symbol.name] = slider
        if symbol.name.startswith(R"\Gamma_{K"):
            categorized_sliders_gamma[0].append(slider)
        elif symbol.name.startswith(R"\Gamma_{\S"):
            categorized_sliders_gamma[1].append(slider)
        elif symbol.name.startswith(R"\Gamma_{N"):
            categorized_sliders_gamma[2].append(slider)

    if symbol.name.startswith("m_{"):
        slider = w.FloatSlider(
            description=Rf"\({sp.latex(symbol)}\)",
            min=0.63,
            max=4,
            step=0.01,
            value=value,
            continuous_update=False,
        )
        sliders[symbol.name] = slider
        if symbol.name.startswith("m_{K"):
            categorized_sliders_m[0].append(slider)
        elif symbol.name.startswith(R"m_{\S"):
            categorized_sliders_m[1].append(slider)
        elif symbol.name.startswith("m_{N"):
            categorized_sliders_m[2].append(slider)

    if symbol.name.startswith("C_{"):
        c_latex = sp.latex(symbol)
        phi_latex = c_latex.replace("C", R"\phi", 1)

        slider_c = w.FloatSlider(
            description=Rf"\({c_latex}\)",
            min=0,
            max=10,
            step=0.01,
            value=abs(value),
            continuous_update=False,
        )
        slider_phi = w.FloatSlider(
            description=Rf"\({phi_latex}\)",
            min=-np.pi,
            max=+np.pi,
            step=0.01,
            value=np.angle(value),
            continuous_update=False,
        )

        sliders[symbol.name] = slider_c
        sliders[symbol.name.replace("C", "phi", 1)] = slider_phi

        cphi_hbox = w.HBox([slider_c, slider_phi])
        if "Sigma" in symbol.name:
            categorized_cphi_pair[1].append(cphi_hbox)
        elif R"\to N" in symbol.name:
            categorized_cphi_pair[2].append(cphi_hbox)
        else:
            categorized_cphi_pair[0].append(cphi_hbox)


assert len(categorized_sliders_gamma) == 3
assert len(categorized_sliders_m) == 3
assert len(categorized_cphi_pair) == 3

subtabs = {}
for category, resonance_list in resonances.items():
    subtabs[category] = []
    for particle in resonance_list:
        m_sliders = [
            slider
            for slider in categorized_sliders_m[category]
            if particle.latex in slider.description
        ]
        gamma_sliders = [
            slider
            for slider in categorized_sliders_gamma[category]
            if particle.latex in slider.description
        ]
        cphi_pairs = [
            hbox
            for hbox in categorized_cphi_pair[category]
            if particle.latex in hbox.children[0].description
        ]
        pole_pair = w.HBox(m_sliders + gamma_sliders)
        resonance_tab = w.VBox([pole_pair, *cphi_pairs])
        subtabs[category].append(resonance_tab)
assert len(subtabs) == 3

main_tabs = []
for category, slider_boxes in subtabs.items():
    sub_tab_widget = w.Tab(children=slider_boxes)
    for i, particle in enumerate(resonances[category]):
        sub_tab_widget.set_title(i, particle.name)

    main_tabs.append(sub_tab_widget)

UI = w.Tab(children=main_tabs, titles=("K*", "Σ*", "N*"))

def insert_phi(parameters: dict) -> dict:
    updated_parameters = {}
    for key, value in parameters.items():
        if key.startswith("phi_"):
            continue
        if key.startswith("C_"):
            phi_key = key.replace("C_", "phi_")
            if phi_key in parameters:
                phi = parameters[phi_key]
                value *= np.exp(1j * phi)  # noqa:PLW2901
        updated_parameters[key] = value
    return updated_parameters

Show code cell source Hide code cell source

%matplotlib widget
%config InlineBackend.figure_formats = ['png']
fig_2d, ax_2d = plt.subplots(dpi=200)
ax_2d.set_title("Model-weighted Phase space Dalitz Plot")
ax_2d.set_xlabel(R"$m^2(\Lambda K^+)\;\left[\mathrm{GeV}^2\right]$")
ax_2d.set_ylabel(R"$m^2(K^+ \pi^0)\;\left[\mathrm{GeV}^2\right]$")

mesh = None


def update_histogram(**parameters):
    global mesh
    parameters = insert_phi(parameters)
    intensity_func.update_parameters(parameters)
    intensity_weights = intensity_func(phsp)
    bin_values, xedges, yedges = jnp.histogram2d(
        phsp["m_01"].real ** 2,
        phsp["m_12"].real ** 2,
        bins=200,
        weights=intensity_weights,
        density=True,
    )
    bin_values = jnp.where(bin_values < 1e-6, jnp.nan, bin_values)
    x, y = jnp.meshgrid(xedges[:-1], yedges[:-1])
    if mesh is None:
        mesh = ax_2d.pcolormesh(x, y, bin_values.T, cmap="jet", vmax=0.15)
    else:
        mesh.set_array(bin_values.T)
    fig_2d.canvas.draw_idle()


interactive_plot = w.interactive_output(update_histogram, sliders)
fig_2d.tight_layout()
fig_2d.colorbar(mesh, ax=ax_2d)

if STATIC_PAGE:
    filename = "dalitz-plot.png"
    fig_2d.savefig(filename)
    plt.close(fig_2d)
    display(UI, Image(filename))
else:
    display(UI, interactive_plot)

Show code cell source Hide code cell source

%matplotlib widget
%config InlineBackend.figure_formats = ['svg']

fig, axes = plt.subplots(figsize=(11, 3.5), ncols=3, sharey=True)
fig.canvas.toolbar_visible = False
fig.canvas.header_visible = False
fig.canvas.footer_visible = False
ax1, ax2, ax3 = axes

for recoil_id, ax in enumerate(axes):
    decay_products = sorted({0, 1, 2} - {recoil_id})
    product_latex = " ".join([reaction.final_state[i].latex for i in decay_products])
    ax.set_xlabel(f"$m({product_latex})$ [GeV]")

LINES = 3 * [None]
RESONANCE_LINE = [None] * len(reaction.get_intermediate_particles())


def update_plot(**parameters):
    parameters = insert_phi(parameters)
    intensity_func.update_parameters(parameters)
    intensities = intensity_func(phsp)
    max_value = 0
    color_id = 0
    for recoil_id, ax in enumerate(axes):
        decay_products = sorted({0, 1, 2} - {recoil_id})
        key = f"m_{''.join(str(i) for i in decay_products)}"
        bin_values, bin_edges = jax.numpy.histogram(
            phsp[key].real,
            bins=120,
            density=True,
            weights=intensities,
        )
        max_value = max(max_value, bin_values.max())

        if LINES[recoil_id] is None:
            LINES[recoil_id] = ax.step(bin_edges[:-1], bin_values, alpha=0.5)[0]
        else:
            LINES[recoil_id].set_ydata(bin_values)

        for resonance in resonances[recoil_id]:
            key = f"m_{{{resonance.latex}}}"
            val = parameters.get(key, resonance.mass)
            if RESONANCE_LINE[color_id] is None:
                RESONANCE_LINE[color_id] = ax.axvline(
                    val,
                    c=f"C{color_id}",
                    ls="dotted",
                    label=resonance.name,
                )
            else:
                RESONANCE_LINE[color_id].set_xdata([val, val])
            color_id += 1

    for ax in axes:
        ax.set_ylim(0, max_value * 1.1)


interactive_plot = w.interactive_output(update_plot, sliders)
for ax in axes:
    ax.legend(fontsize="small")
fig.tight_layout()

if STATIC_PAGE:
    filename = "histogram.svg"
    fig.savefig(filename)
    plt.close(fig)
    display(UI, SVG(filename))
else:
    display(UI, interactive_plot)