TR-025

Rotated square root cut

Investigation of the branch cut in the two Riemann sheets of a square root and what happens if the cut is rotated around \(z=0\).

✅ compwa.github.io#236

Rotating square root cuts

Show code cell content Hide code cell content

import os
from typing import Any

import matplotlib.pyplot as plt
import numpy as np
import plotly.graph_objects as go
import sympy as sp
from ampform.io import aslatex
from ampform.sympy import unevaluated
from IPython.display import Image, Math, display
from ipywidgets import FloatSlider, VBox, interactive_output
from plotly.colors import DEFAULT_PLOTLY_COLORS
from plotly.subplots import make_subplots

STATIC_WEB_PAGE = {"EXECUTE_NB", "READTHEDOCS"}.intersection(os.environ)

See also

Lecture 17 on collision theory of the STRONG2020 HaSP School by Miguel Albaladejo.

There are multiple solutions for \(x\) to the equation \(y^2 = x\). The fact that we usually take \(y = \sqrt{x}\) with \(\sqrt{-1} = i\) to be ‘the’ solution to this equation is just a matter of convention. It would be more complete to represent the solution as a set of points in the complex plane, that is, the set \(S = \left\{\left(z, w\right)\in\mathbb{C}^2 | w^2=z\right\}\). This is set forms a Riemann surface in \(\mathbb{C}^2\) space.

In the figure below we see the Riemann surface of a square root in \(\mathbb{C}^2\) space. The \(xy\) plane forms the complex domain \(\mathbb{C}\), the \(z\) axis indicates the imaginary part of the Riemann surface and the color indicates the real part.

Show code cell source Hide code cell source

resolution = 30
R, Θ = np.meshgrid(
    np.linspace(0, 1, num=resolution),
    np.linspace(-np.pi, +np.pi, num=resolution),
)
X = R * np.cos(Θ)
Y = R * np.sin(Θ)
Z = X + Y * 1j
T = np.sqrt(Z)
style = lambda t: dict(
    cmin=-1,
    cmax=+1,
    colorscale="RdBu_r",
    surfacecolor=t.real,
)
fig = go.Figure([
    go.Surface(x=X, y=Y, z=+T.imag, **style(+T), name="+√z"),
    go.Surface(x=X, y=Y, z=-T.imag, **style(-T), name="-√z", showscale=False),
])
fig.update_traces(selector=0, colorbar=dict(title="Re ±√z"))
fig.update_layout(
    height=550,
    margin=dict(l=0, r=0, t=30, b=0, pad=0),
    title_text="Riemann surface of a square root",
    title_x=0.5,
)
fig.update_scenes(
    camera_center=dict(z=-0.1),
    camera_eye=dict(x=1.4, y=1.4, z=1.4),
    xaxis_title="Re z",
    yaxis_title="Im z",
    zaxis_title="Im ±√z",
)
fig.show()

From this figure it becomes clear that it is impossible to define one single-valued function that gives the solution to \(w^2 = u\) is \(w \neq 0\). The familiar single-valued square root operation \(\sqrt{}\) covers only one segment, or sheet, of the Riemann surface and it is defined in such a way that \(\sqrt{-1}=i\). The other half of the surface is covered by \(-\sqrt{}\).

Notice, however, that the sheets for the imaginary component of \(\sqrt{}\) are not smoothly connected at each point. The sign flips around \(z\in\mathbb{R^-}\), because we have \(\sqrt{-1+0i}=-1\) and \(\sqrt{-1+0i}=+1\). We call this discontinuity in the Riemann sheet a branch cut.

Show code cell source Hide code cell source

x = np.linspace(-1, 0, num=resolution // 2)
y = np.zeros(resolution // 2)
t = np.sqrt(x + 1e-8j)
T = np.sqrt(Z)

C0 = DEFAULT_PLOTLY_COLORS[0]
C1 = DEFAULT_PLOTLY_COLORS[1]

style = lambda color, legend: dict(
    colorscale=[[0, color], [1, color]],
    showlegend=legend,
    showscale=False,
    surfacecolor=np.ones(T.shape),
)
linestyle = dict(
    line_color="crimson",
    line_showscale=False,
    line_width=15,
    mode="lines",
    name="Branch cut",
)

fig = make_subplots(
    rows=1,
    cols=2,
    horizontal_spacing=0.01,
    subplot_titles=("Re ±√z", "Im ±√z"),
    specs=[[{"type": "surface"}, {"type": "surface"}]],
)
fig.add_traces(
    [
        go.Surface(x=X, y=Y, z=+T.real, **style(C0, True), name="+√z"),
        go.Surface(x=X, y=Y, z=-T.real, **style(C1, True), name="-√z"),
    ],
    cols=1,
    rows=1,
)
fig.add_traces(
    [
        go.Surface(x=X, y=Y, z=+T.imag, **style(C0, False), name="+√z"),
        go.Surface(x=X, y=Y, z=-T.imag, **style(C1, False), name="-√z"),
        go.Scatter3d(x=x, y=y, z=-t.imag, **linestyle, showlegend=True),
        go.Scatter3d(x=x, y=y, z=+t.imag, **linestyle, showlegend=False),
    ],
    cols=2,
    rows=1,
)
ticks = dict(
    tickvals=[-1, 0, +1],
    ticktext=["-1", "0", "+1"],
)
fig.update_layout(
    height=400,
    margin=dict(l=2, r=2, t=20, b=0, pad=0),
)
fig.update_scenes(
    camera_center=dict(z=-0.1),
    camera_eye=dict(x=1.4, y=1.4, z=1.4),
    xaxis=dict(title="Re z", **ticks),
    yaxis=dict(title="Im z", **ticks),
)
fig.update_scenes(selector=0, zaxis=dict(title="Re ±√z", **ticks))
fig.update_scenes(selector=1, zaxis=dict(title="Im ±√z", **ticks))
fig.show()

By definition, the branch cut of \(\sqrt{}\) is located at \(\mathbb{R}^-\). There is no requirement about this definition though: we can segment the Riemann surface in any way into two sheets, as long as the sheets remain single-valued. One option is to rotate the cut. With the following definition, we have a single-value square-root function, where the cut is rotated over an angle \(\phi\) around \(z=0\).

Show code cell source Hide code cell source

@unevaluated
class RotatedSqrt(sp.Expr):
    z: Any
    phi: Any = 0
    _latex_repr_ = R"\sqrt[{phi}]{{{z}}}"

    def evaluate(self) -> sp.Expr:
        z, phi = self.args
        return sp.exp(-phi * sp.I / 2) * sp.sqrt(z * sp.exp(phi * sp.I))


z, phi = sp.symbols("z phi")
expr = RotatedSqrt(z, phi)
Math(aslatex({expr: expr.doit(deep=False)}))

\[\begin{split}\displaystyle \begin{array}{rcl} \sqrt[\phi]{z} &=& \sqrt{z e^{i \phi}} e^{- \frac{i \phi}{2}} \\ \end{array}\end{split}\]

In the following widget, we see what the new rotated square root looks like in the complex plane. The left panes show the imaginary part and the right side shows the real part. The upper figures show the value of the rotated square root on the real axis, \(\mathrm{Re}\,z\).

Show code cell source Hide code cell source

symbols = (z, phi)
func = sp.lambdify(symbols, expr.doit())

mpl_fig, axes = plt.subplots(
    figsize=(12, 8.5),
    gridspec_kw=dict(
        height_ratios=[1, 2],
        width_ratios=[1, 1, 0.03],
    ),
    ncols=3,
    nrows=2,
)
mpl_fig.canvas.toolbar_visible = False
mpl_fig.canvas.header_visible = False
mpl_fig.canvas.footer_visible = False
axes[0, 2].remove()
ax1re, ax2re = axes[:, 0]
ax1im, ax2im = axes[:, 1]
ax_bar = axes[1, 2]
ax1re.set_ylabel(f"${sp.latex(expr)}$")
ax1im.set_title(Rf"$\mathrm{{Im}}\,{sp.latex(expr)}$")
ax1re.set_title(Rf"$\mathrm{{Re}}\,{sp.latex(expr)}$")
ax2re.set_ylabel(R"$\mathrm{Im}\,z$")
for ax in (ax1im, ax1re):
    ax.set_yticks([-1, -0.5, 0, +0.5, +1])
    ax.set_yticklabels(["-1", R"$-\frac{1}{2}$", "0", R"$+\frac{1}{2}$", "+1"])
for ax in axes[:, :2].flatten():
    ax.set_xlabel(R"$\mathrm{Re}\,z$")
    ax.set_xticks([-1, 0, +1])
    ax.set_xticklabels(["-1", "0", "+1"])
    ax.set_yticks([-1, 0, +1])
    ax.set_yticklabels(["-1", "0", "+1"])
for i, ax in enumerate((ax2im, ax2re)):
    ax.axhline(0, c=f"C{i}", ls="dotted", zorder=99)
    ax.set_ylim(-1, +1)

data = None
x = np.linspace(-1, +1, num=400)
X_mpl, Y_mpl = np.meshgrid(x, x)
Z_mpl = X_mpl + Y_mpl * 1j


def plot(phi):
    global data
    mpl_fig.suptitle(Rf"$\phi={phi / np.pi:.4g}\pi$")
    t_mpl = func(x, phi)
    T_mpl = func(Z_mpl, phi)
    if data is None:
        data = {
            "im": ax1im.plot(x, t_mpl.imag, label="imag", c="C0", ls="dotted")[0],
            "re": ax1re.plot(x, t_mpl.real, label="real", c="C1", ls="dotted")[0],
            "im2D": ax2im.pcolormesh(X_mpl, Y_mpl, T_mpl.imag, cmap=plt.cm.coolwarm),
            "re2D": ax2re.pcolormesh(X_mpl, Y_mpl, T_mpl.real, cmap=plt.cm.coolwarm),
        }
    else:
        data["re"].set_ydata(t_mpl.real)
        data["im"].set_ydata(t_mpl.imag)
        data["im2D"].set_array(T_mpl.imag)
        data["re2D"].set_array(T_mpl.real)
    data["im2D"].set_clim(vmin=-1, vmax=+1)
    data["re2D"].set_clim(vmin=-1, vmax=+1)
    ax1im.set_ylim(-1.2, +1.2)
    ax1re.set_ylim(-1.2, +1.2)
    mpl_fig.canvas.draw_idle()


sliders = dict(
    phi=FloatSlider(
        min=-3 * np.pi,
        max=+3 * np.pi,
        step=np.pi / 8,
        description="phi",
        value=-np.pi / 4,
    ),
)
ui = VBox(tuple(sliders.values()))
output = interactive_output(plot, controls=sliders)
cbar = plt.colorbar(data["re2D"], cax=ax_bar)
cbar.ax.set_xlabel(f"${sp.latex(expr)}$")
cbar.ax.set_yticks([-1, 0, +1])
mpl_fig.tight_layout()
display(ui, output)

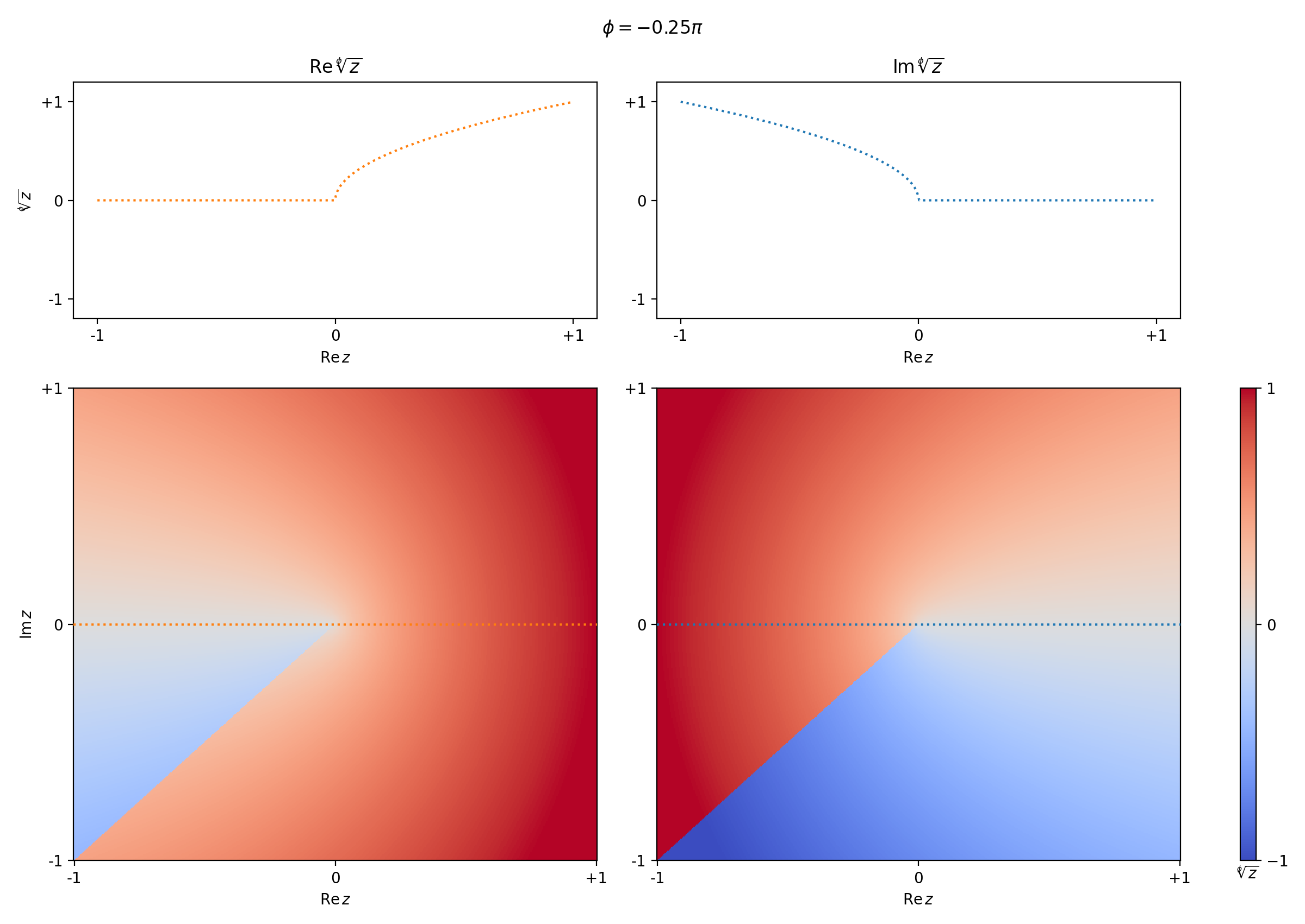
Note

The real part does not have a cut if \(\phi = 2\pi n, n \in \mathbb{Z}\). The cut in the imaginary part disappears if \(\phi = \pi + 2\pi n\).