Analyticity

Analyticity#

Branch points of \(\rho(s)\)#

Investigation of Section 2.1.2 in [Aitchison, 2015].

\[\displaystyle \frac{\sqrt{\frac{\left(s - \left(m_{1} - m_{2}\right)^{2}\right) \left(s - \left(m_{1} + m_{2}\right)^{2}\right)}{s}}}{\sqrt{s}}\]

Or, assuming both decay products to be of unit mass:

\[\displaystyle \frac{\sqrt{s - 4}}{\sqrt{s}}\]

../_images/e77746bf49489a29f2a6f0aeb48d79d96c3d4ac8f1ce835db0b7be05394c95e9.png

<Figure size 640x480 with 0 Axes>

../_images/abe7b65399792a7776c341a938e32cbc47071179d3232fa13fdecb2309464d4b.png

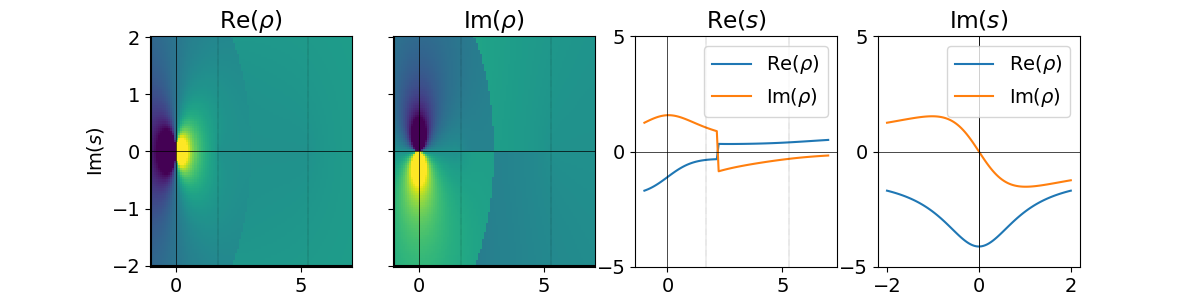
Physical vs. unphysical sheet#

Interactive reproduction of Figure 49.1 on PDG2020, §Resonances, p.2. The formulas below come from a relativistic_breit_wigner_with_ff() with \(L=0\). As phase space factor, we used the square root of BreakupMomentumSquared instead of the default PhaseSpaceFactor, because this introduces only one branch point in the \(s\)-plane (namely the one over the nominator).

\[\displaystyle \mathrm{Physical:} \quad \frac{\Gamma_{0} m_{0}}{\Gamma_{0} m_{0}^{2} \sqrt{- \frac{\left(s - \left(m_{1} - m_{2}\right)^{2}\right) \left(s - \left(m_{1} + m_{2}\right)^{2}\right)}{s \left(m_{0}^{2} - \left(m_{1} - m_{2}\right)^{2}\right) \left(m_{0}^{2} - \left(m_{1} + m_{2}\right)^{2}\right)}} + m_{0}^{2} - s}\]

\[\displaystyle \mathrm{Unphysical:} \quad \frac{\Gamma_{0} m_{0}}{- \frac{i \Gamma_{0} m_{0}^{2} \sqrt{\frac{\left(s - \left(m_{1} - m_{2}\right)^{2}\right) \left(s - \left(m_{1} + m_{2}\right)^{2}\right)}{s}}}{\sqrt{\left(m_{0}^{2} - \left(m_{1} - m_{2}\right)^{2}\right) \left(m_{0}^{2} - \left(m_{1} + m_{2}\right)^{2}\right)}} + m_{0}^{2} - s}\]

Show code cell source Hide code cell source

args = (s, m0, gamma0, m1, m2)
np_amp_physical = sp.lambdify(args, physical_amp, "numpy")
np_amp_unphysical = sp.lambdify(args, unphysical_amp, "numpy")

x_min, x_max = -0.2, 1.3
y_min, y_max = -1.8, +1.8
z_min, z_max = -2.5, +2.5

x = np.linspace(x_min, x_max, num=50)
y_neg = np.linspace(y_min, -1e-4, num=30)
y_pos = np.linspace(1e-4, y_max, num=30)

X, Y_neg = np.meshgrid(x, y_neg)
X, Y_pos = np.meshgrid(x, y_pos)
s_values_neg = X + Y_neg * 1j
s_values_pos = X + Y_pos * 1j

z_cut_min = 0.75 * z_min
z_cut_max = 0.75 * z_max
cut_off_min = np.vectorize(lambda z: max(z_cut_min, z))
cut_off_max = np.vectorize(lambda z: min(z_cut_max, z))

plot_style = {
    "linewidth": 0,
    "alpha": 0.7,
    "antialiased": True,
    "rstride": 1,
    "cstride": 1,
}
axis_style = {
    "c": "black",
    "linewidth": 0.7,
    "linestyle": "dashed",
}

fig, axes = plt.subplots(
    ncols=2,
    figsize=(10, 6),
    subplot_kw={"projection": "3d"},
    tight_layout=True,
)
ax1, ax2 = axes
fig.suptitle("$S$-wave Breit-Wigner ($L=0$) plotted over the complex $s$-plane")

m0_min = np.sign(x_min) * np.sqrt(np.abs(x_min))
m0_max = np.sign(x_max) * np.sqrt(np.abs(x_max))

sliders = {
    "m0": widgets.FloatSlider(
        min=m0_min,
        max=m0_max,
        value=0.8,
        step=0.01,
        description="$m_0$",
    ),
    "gamma0": widgets.FloatSlider(
        min=0.0,
        max=y_max,
        value=0.3,
        step=0.01,
        description=R"$\Gamma_0$",
    ),
    "m1": widgets.FloatSlider(
        min=1e-4,
        max=m0_max / 2,
        step=0.01,
        description="$m_1$",
    ),
    "m2": widgets.FloatSlider(
        min=1e-4,
        max=m0_max / 2,
        step=0.01,
        description="$m_2$",
    ),
}


@widgets.interact(**sliders)
def plot(m0, gamma0, m1, m2):
    def plot_expression(ax, amp, neg_color="green"):
        ax.clear()
        z_values_neg = amp(s_values_neg, m0, gamma0, m1, m2).imag
        z_values_pos = amp(s_values_pos, m0, gamma0, m1, m2).imag
        Z_neg = cut_off_min(cut_off_max(z_values_neg))
        Z_pos = cut_off_min(cut_off_max(z_values_pos))

        s_thr = (m1 + m2) ** 2
        x0 = x[x >= s_thr] + 1e-4j
        y0 = np.zeros(len(x0))
        z0 = amp(x0, m0, gamma0, m1, m2).imag

        ax.plot_surface(X, Y_neg, Z_neg, **plot_style, color=neg_color)
        ax.plot_surface(X, Y_pos, Z_pos, **plot_style, color="green")
        ax.plot(x0, y0, z0, linewidth=2.5, c="darkred", zorder=8)
        ax.scatter([x0[0]], [0], [z0[0]], c="darkred", s=20, zorder=9)

        ax.set_xlabel("Re($s$)", labelpad=-15)
        ax.set_ylabel("Im($s$)", labelpad=-15)
        ax.set_zlabel("Im($A$)", labelpad=-15)
        ax.set_xticks([])
        ax.set_yticks([])
        ax.set_zticks([])
        ax.set_zlim(z_min, z_max)

    plot_expression(ax1, np_amp_physical)
    plot_expression(ax2, np_amp_unphysical, neg_color="gold")

    ax1.text(x_min, y_max, z_max / 2, "physical sheet", c="green")
    ax2.text(x_min, y_min, -z_max, "unphysical sheet", c="gold")

    fig.canvas.draw_idle()

../_images/b07ad5bbcdaa640ff34236ec945aaebc1770fa130bd5427492e0f6871a15eaa2.svg

Analyticity

Contents

Analyticity#

Branch points of \(\rho(s)\)#

Physical vs. unphysical sheet#