Coupled channel Riemann sheets

Coupled channel Riemann sheets#

Expression definitions#

\[\begin{split}\displaystyle \begin{array}{rcl} \rho_{m_{1}, m_{2}}\left(s\right) &=& \sqrt{\frac{\left(s - \left(m_{1} - m_{2}\right)^{2}\right) \left(s - \left(m_{1} + m_{2}\right)^{2}\right)}{s^{2}}} \\ \end{array}\end{split}\]

\[\begin{split}\displaystyle \begin{array}{rcl} \rho_{m_{1}, m_{2}}\left(s\right) &=& \frac{2 q\left(s\right)}{\sqrt{s}} \\ \rho^\mathrm{CM}_{m_{1},m_{2}}\left(s\right) &=& - 16 i \pi \Sigma\left(s\right) \\ \Sigma\left(s\right) &=& \frac{- \left(m_{1}^{2} - m_{2}^{2}\right) \left(- \frac{1}{\left(m_{1} + m_{2}\right)^{2}} + \frac{1}{s}\right) \log{\left(\frac{m_{1}}{m_{2}} \right)} + \frac{2 \log{\left(\frac{m_{1}^{2} + m_{2}^{2} + 2 \sqrt{s} q\left(s\right) - s}{2 m_{1} m_{2}} \right)} q\left(s\right)}{\sqrt{s}}}{16 \pi^{2}} \\ q\left(s\right) &=& \frac{\sqrt{\lambda\left(s, m_{1}^{2}, m_{2}^{2}\right)}}{2 \sqrt{s}} \\ \lambda\left(x, y, z\right) &=& x^{2} - 2 x y - 2 x z + y^{2} - 2 y z + z^{2} \\ \end{array}\end{split}\]

Riemann sheet I#

Matrix definition#

\[\begin{split}\displaystyle \begin{array}{rcl} \rho^{\Sigma} &=& \left[\begin{matrix}{\rho^{\Sigma}}_{0,0} & 0\\0 & {\rho^{\Sigma}}_{1,1}\end{matrix}\right] \\ \end{array}\end{split}\]

T_I = (I - sp.I * K * CM).inv() * K
T_I

\[\displaystyle \left(\mathbb{I} + - i K \rho^{\Sigma}\right)^{-1} K\]

T_I_explicit = T_I.as_explicit()
T_I_explicit[0, 0].simplify(doit=False)

\[\displaystyle \frac{\left(i {K}_{1,1} {\rho^{\Sigma}}_{1,1} - 1\right) {K}_{0,0} - i {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{1,1}}{{K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{0,0} {\rho^{\Sigma}}_{1,1} + i {K}_{0,0} {\rho^{\Sigma}}_{0,0} - {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{0,0} {\rho^{\Sigma}}_{1,1} + i {K}_{1,1} {\rho^{\Sigma}}_{1,1} - 1}\]

Parametrization#

\[\begin{split}\displaystyle \begin{array}{rcl} {K}_{0,0} &=& \frac{\left(g^{0}_1\right)^{2} m_{0}}{- m_{0}^{2} + s} \\ {K}_{1,1} &=& \frac{\left(g^{0}_2\right)^{2} m_{0}}{- m_{0}^{2} + s} \\ {K}_{0,1} &=& \frac{g^{0}_1 g^{0}_2 m_{0}}{- m_{0}^{2} + s} \\ {K}_{1,0} &=& \frac{g^{0}_1 g^{0}_2 m_{0}}{- m_{0}^{2} + s} \\ {\rho^{\Sigma}}_{0,0} &=& - \rho^\mathrm{CM}_{m_{a1},m_{b1}}\left(s\right) \\ {\rho^{\Sigma}}_{1,1} &=& - \rho^\mathrm{CM}_{m_{a2},m_{b2}}\left(s\right) \\ \end{array}\end{split}\]

T_I_cm_expr = T_I_explicit.xreplace(cm_expressions)
T_I_cm_expr[0, 0].simplify(doit=False)

\[\displaystyle \frac{\left(g^{0}_1\right)^{2} m_{0}}{i \left(g^{0}_1\right)^{2} m_{0} \rho^\mathrm{CM}_{m_{a1},m_{b1}}\left(s\right) + i \left(g^{0}_2\right)^{2} m_{0} \rho^\mathrm{CM}_{m_{a2},m_{b2}}\left(s\right) - m_{0}^{2} + s}\]

Sheets II, III, and IV#

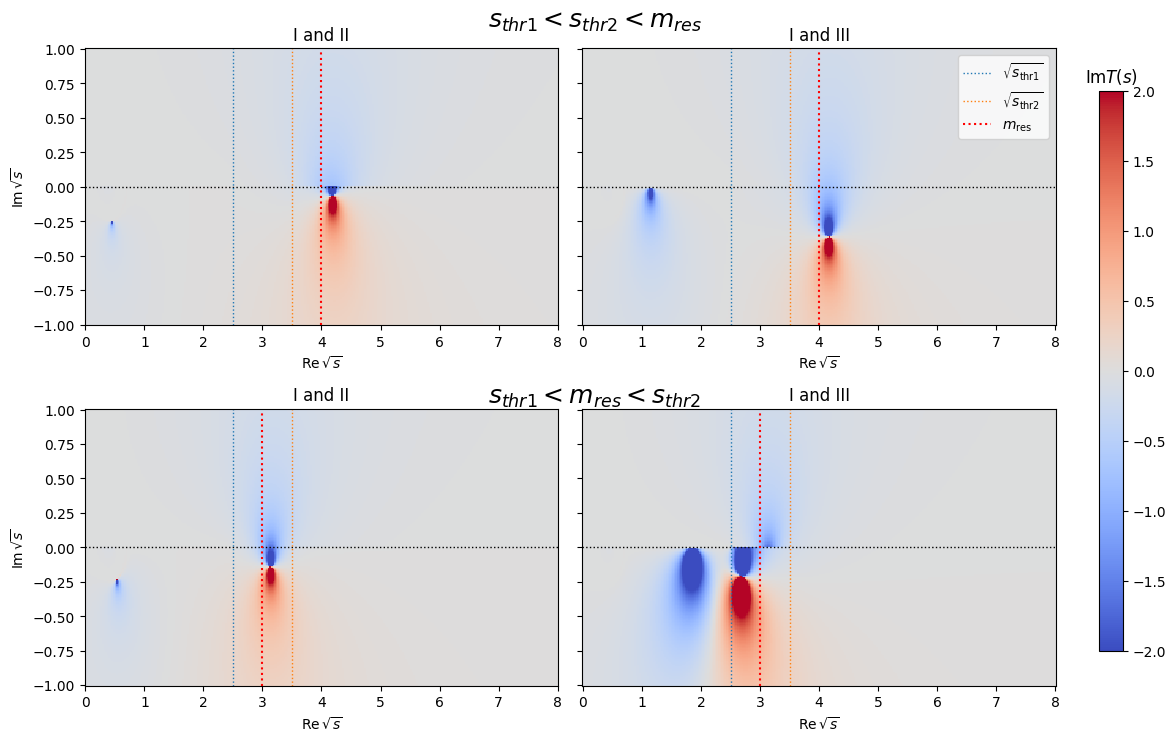
In the case of two channels, there are four Riemann sheets. The first sheet (Sheet I) is physical and three unphysical ones. The physical sheet is calculated using the analytic solution of the Chew-Mandelstam function.

\[\begin{split} \begin{eqnarray} \operatorname{Disc}_{\mathrm{I,II}} T_K^{-1} &=& 2 i\left[\begin{array}{rr}\rho_1 & 0 \\ 0 & 0 \end{array}\right], \\ \operatorname{Disc}_{\mathrm{I,III}} T_K^{-1} &=& 2 i\left[\begin{array}{rr}\rho_1 & 0 \\ 0 & \rho_2 \end{array}\right], \\ \operatorname{Disc}_{\mathrm{I,IV}} T_K^{-1} &=& 2 i\left[\begin{array}{rr}0 & 0 \\ 0& \rho_2 \end{array}\right]. \end{eqnarray} \end{split}\]

Depending on the centre-of-mass energy, different Riemann sheets connect smoothly to the physical one. Therefore, two cases are studied: one where the resonance mass is above the threshold of the second and first channel, and another where the resonance mass is between the threshold of the first and second channel.

\[\begin{split}\displaystyle \begin{array}{rcl} \rho &=& \left[\begin{matrix}{\rho}_{0,0} & 0\\0 & {\rho}_{1,1}\end{matrix}\right] \\ \end{array}\end{split}\]

T_II = (T_I.inv() + 2 * sp.I * rho).inv()
T_III = (T_I.inv() + 2 * sp.I * rho).inv()
T_IV = (-T_I.inv() - 2 * sp.I * rho).inv()
Math(aslatex([T_II, T_III, T_IV]))

\[\begin{split}\displaystyle \begin{array}{c} \left(2 i \rho + K^{-1} \left(\mathbb{I} + - i K \rho^{\Sigma}\right)\right)^{-1} \\ \left(2 i \rho + K^{-1} \left(\mathbb{I} + - i K \rho^{\Sigma}\right)\right)^{-1} \\ \left(- 2 i \rho - K^{-1} \left(\mathbb{I} + - i K \rho^{\Sigma}\right)\right)^{-1} \\ \end{array}\end{split}\]

T_II_explicit = T_II.as_explicit()
T_II_explicit[0, 0].simplify(doit=False)

\[\displaystyle \frac{- i {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{1,1} + 2 i {K}_{0,0} {K}_{1,1} {\rho}_{1,1} + {K}_{0,0} + i {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{1,1} - 2 i {K}_{0,1} {K}_{1,0} {\rho}_{1,1}}{- {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{0,0} {\rho^{\Sigma}}_{1,1} + 2 {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{0,0} {\rho}_{1,1} + 2 {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{1,1} {\rho}_{0,0} - 4 {K}_{0,0} {K}_{1,1} {\rho}_{0,0} {\rho}_{1,1} - i {K}_{0,0} {\rho^{\Sigma}}_{0,0} + 2 i {K}_{0,0} {\rho}_{0,0} + {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{0,0} {\rho^{\Sigma}}_{1,1} - 2 {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{0,0} {\rho}_{1,1} - 2 {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{1,1} {\rho}_{0,0} + 4 {K}_{0,1} {K}_{1,0} {\rho}_{0,0} {\rho}_{1,1} - i {K}_{1,1} {\rho^{\Sigma}}_{1,1} + 2 i {K}_{1,1} {\rho}_{1,1} + 1}\]

T_III_explicit = T_III.as_explicit()
T_III_explicit[0, 0].simplify(doit=False)

\[\displaystyle \frac{- i {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{1,1} + 2 i {K}_{0,0} {K}_{1,1} {\rho}_{1,1} + {K}_{0,0} + i {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{1,1} - 2 i {K}_{0,1} {K}_{1,0} {\rho}_{1,1}}{- {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{0,0} {\rho^{\Sigma}}_{1,1} + 2 {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{0,0} {\rho}_{1,1} + 2 {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{1,1} {\rho}_{0,0} - 4 {K}_{0,0} {K}_{1,1} {\rho}_{0,0} {\rho}_{1,1} - i {K}_{0,0} {\rho^{\Sigma}}_{0,0} + 2 i {K}_{0,0} {\rho}_{0,0} + {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{0,0} {\rho^{\Sigma}}_{1,1} - 2 {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{0,0} {\rho}_{1,1} - 2 {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{1,1} {\rho}_{0,0} + 4 {K}_{0,1} {K}_{1,0} {\rho}_{0,0} {\rho}_{1,1} - i {K}_{1,1} {\rho^{\Sigma}}_{1,1} + 2 i {K}_{1,1} {\rho}_{1,1} + 1}\]

T_IV_explicit = T_IV.as_explicit()
T_IV_explicit[0, 0].simplify(doit=False)

\[\displaystyle \frac{i {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{1,1} - 2 i {K}_{0,0} {K}_{1,1} {\rho}_{1,1} - {K}_{0,0} - i {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{1,1} + 2 i {K}_{0,1} {K}_{1,0} {\rho}_{1,1}}{- {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{0,0} {\rho^{\Sigma}}_{1,1} + 2 {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{0,0} {\rho}_{1,1} + 2 {K}_{0,0} {K}_{1,1} {\rho^{\Sigma}}_{1,1} {\rho}_{0,0} - 4 {K}_{0,0} {K}_{1,1} {\rho}_{0,0} {\rho}_{1,1} - i {K}_{0,0} {\rho^{\Sigma}}_{0,0} + 2 i {K}_{0,0} {\rho}_{0,0} + {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{0,0} {\rho^{\Sigma}}_{1,1} - 2 {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{0,0} {\rho}_{1,1} - 2 {K}_{0,1} {K}_{1,0} {\rho^{\Sigma}}_{1,1} {\rho}_{0,0} + 4 {K}_{0,1} {K}_{1,0} {\rho}_{0,0} {\rho}_{1,1} - i {K}_{1,1} {\rho^{\Sigma}}_{1,1} + 2 i {K}_{1,1} {\rho}_{1,1} + 1}\]

rho_expressions_II = {
    **cm_expressions,
    rho[0, 0]: PhaseSpaceFactor(s, ma1, mb1),
    rho[1, 1]: 0,
}
rho_expressions_III = {
    **cm_expressions,
    rho[0, 0]: PhaseSpaceFactor(s, ma1, mb1),
    rho[1, 1]: PhaseSpaceFactor(s, ma2, mb2),
}
rho_expressions_IV = {
    **cm_expressions,
    rho[0, 0]: 0,
    rho[1, 1]: PhaseSpaceFactor(s, ma2, mb2),
}

# @title
T_II_rho_expr = T_II_explicit.xreplace(rho_expressions_II)
T_III_rho_expr = T_III_explicit.xreplace(rho_expressions_III)
T_IV_rho_expr = T_IV_explicit.xreplace(rho_expressions_IV)

T_II_rho_expr[0, 0].simplify(doit=False)

\[\displaystyle \frac{\left(g^{0}_1\right)^{2} m_{0}}{i \left(g^{0}_1\right)^{2} m_{0} \rho^\mathrm{CM}_{m_{a1},m_{b1}}\left(s\right) + 2 i \left(g^{0}_1\right)^{2} m_{0} \rho_{m_{a1}, m_{b1}}\left(s\right) + i \left(g^{0}_2\right)^{2} m_{0} \rho^\mathrm{CM}_{m_{a2},m_{b2}}\left(s\right) - m_{0}^{2} + s}\]

T_III_rho_expr[0, 0].simplify(doit=False)

\[\displaystyle \frac{\left(g^{0}_1\right)^{2} m_{0}}{i \left(g^{0}_1\right)^{2} m_{0} \rho^\mathrm{CM}_{m_{a1},m_{b1}}\left(s\right) + 2 i \left(g^{0}_1\right)^{2} m_{0} \rho_{m_{a1}, m_{b1}}\left(s\right) + i \left(g^{0}_2\right)^{2} m_{0} \rho^\mathrm{CM}_{m_{a2},m_{b2}}\left(s\right) + 2 i \left(g^{0}_2\right)^{2} m_{0} \rho_{m_{a2}, m_{b2}}\left(s\right) - m_{0}^{2} + s}\]

Visualizations#

Lineshapes (real axis)#

Show code cell source Hide code cell source

# @title
%config InlineBackend.figure_formats = ["svg"]

T_I_func = sp.lambdify(symbols, T_I_cm_expr[0, 0].doit())
T_II_func = sp.lambdify(symbols, T_II_rho_expr[0, 0].doit())
T_III_func = sp.lambdify(symbols, T_III_rho_expr[0, 0].doit())
T_IV_func = sp.lambdify(symbols, T_IV_rho_expr[0, 0].doit())
parameter_defaults1 = {
    ma1: 1.0,
    mb1: 1.5,
    ma2: 1.5,
    mb2: 2.0,
    m0: 4.0,
    g1: 0.7,
    g2: 0.7,
}
parameter_defaults2 = {
    **parameter_defaults1,
    m0: 3.0,
}
args1 = eval(str(symbols[1:].xreplace(parameter_defaults1)))
args2 = eval(str(symbols[1:].xreplace(parameter_defaults2)))

epsilon = 1e-5
x = np.linspace(0, 8, num=300)
y = np.linspace(epsilon, 1, num=100)
X, Y = np.meshgrid(x, y)
Zn = X - Y * 1j
Zp = X + Y * 1j

T1n_res1 = T_I_func(Zn**2, *args1)
T1p_res1 = T_I_func(Zp**2, *args1)

T2n_res1 = T_II_func(Zn**2, *args1)
T2p_res1 = T_II_func(Zp**2, *args1)

T3n_res1 = T_III_func(Zn**2, *args1)
T3p_res1 = T_III_func(Zp**2, *args1)

T4n_res1 = T_IV_func(Zn**2, *args1)
T4p_res1 = T_IV_func(Zp**2, *args1)

T1n_res2 = T_I_func(Zn**2, *args2)
T1p_res2 = T_I_func(Zp**2, *args2)

T2n_res2 = T_II_func(Zn**2, *args2)
T2p_res2 = T_II_func(Zp**2, *args2)

T3n_res2 = T_III_func(Zn**2, *args2)
T3p_res2 = T_III_func(Zp**2, *args2)

T4n_res2 = T_IV_func(Zn**2, *args2)
T4p_res2 = T_IV_func(Zp**2, *args2)

fig, axes = plt.subplots(figsize=(11, 6), ncols=4, sharey=True)
ax1, ax2, ax3, ax4 = axes.flatten()

ax1.plot(x, T1n_res1[0].imag, label=R"$T_\mathrm{I}(s-0i)$")
ax1.plot(x, T1p_res1[0].imag, label=R"$T_\mathrm{I}(s+0i)$")
ax1.set_title(f"${sp.latex(rho_cm_expr)}$")
ax1.set_title(R"$T_\mathrm{I}$")

ax2.plot(x, T2n_res1[0].imag, label=R"$T_\mathrm{II}(s-0i)$")
ax2.plot(x, T2p_res1[0].imag, label=R"$T_\mathrm{II}(s+0i)$")
ax2.set_title(R"$T_\mathrm{II}$")

ax3.plot(x, T3n_res1[0].imag, label=R"$T_\mathrm{III}(s-0i)$")
ax3.plot(x, T3p_res1[0].imag, label=R"$T_\mathrm{III}(s+0i)$")
ax3.set_title(R"$T_\mathrm{III}$")

ax4.plot(x, T4n_res1[0].imag, label=R"$T_\mathrm{III}(s-0i)$")
ax4.plot(x, T4p_res1[0].imag, label=R"$T_\mathrm{IV}(s+0i)$")
ax4.set_title(R"$T_\mathrm{III}$")

for ax in axes:
    ax.legend()
    ax.set_xlabel(R"$\mathrm{Re}\,\sqrt{s}$")
    ax.set_ylim(-1, +1)
ax1.set_ylabel(R"$\mathrm{Im}\,T(s)$ (a.u.)")

fig.tight_layout()
plt.show()

../_images/bfece35f3fa392b665848ed6e3c0b39cd9d47ca7f335f83c4f33e5a387cad889.svg

Complex plane (2D)#

It can be shown that if the resonance mass is above both thresholds the third sheet connects smoothly to the first sheet. If the resonance mass is above the first and below the second threshold the second sheet transitions smoothly into the first sheet.

../_images/096a06307ce040be62905785ca4acd69113de30b42a1c5a17c5028f76c75f26d.png

Riemann sheets (3D)#

Show code cell source Hide code cell source

# @title
Sp_I_res1 = go.Surface(x=X, y=+Y, z=T1p_res1.imag, **sty("T1 (physical)"))
Sn_II_res1 = go.Surface(x=X, y=-Y, z=T2n_res1.imag, **sty("T2 (unphysical)"))
Sn_III_res1 = go.Surface(x=X, y=-Y, z=T3n_res1.imag, **sty("T3 (unphysical)"))

Sp_I_res2 = go.Surface(x=X, y=+Y, z=T1p_res2.imag, **sty("T1 (physical)"))
Sn_II_res2 = go.Surface(x=X, y=-Y, z=T2n_res2.imag, **sty("T2 (unphysical)"))
Sn_III_res2 = go.Surface(x=X, y=-Y, z=T3n_res2.imag, **sty("T3 (unphysical)"))

thr1_filter = x >= s_thr1
thr2_filter = x >= s_thr2

line_kwargs = dict(
    line=dict(color="yellow", width=8),
    mode="lines",
    name="Lineshape",
)
lineshape_res1_z = project(T1p_res1[0])
lineshape_res2_z = project(T1p_res2[0])
lineshape_res1 = go.Scatter3d(
    x=x[thr1_filter],
    y=np.zeros(thr1_filter.shape),
    z=lineshape_res1_z[thr1_filter],
    **line_kwargs,
)
lineshape_res2 = go.Scatter3d(
    x=x[thr1_filter],
    y=np.zeros(thr1_filter.shape),
    z=lineshape_res2_z[thr1_filter],
    **line_kwargs,
)

point_kwargs = dict(
    hoverinfo="text",
    marker=dict(color=DEFAULT_PLOTLY_COLORS[:2], size=6),
    mode="markers",
    text=["threshold 1", "threshold 2"],
)
thr_points_res1 = go.Scatter3d(
    x=[s_thr1, s_thr2],
    y=[0, 0],
    z=[lineshape_res1_z[thr1_filter][0], lineshape_res1_z[thr2_filter][0]],
    **point_kwargs,
)
thr_points_res2 = go.Scatter3d(
    x=[s_thr1, s_thr2],
    y=[0, 0],
    z=[lineshape_res2_z[thr1_filter][0], lineshape_res2_z[thr2_filter][0]],
    **point_kwargs,
)

plotly_fig = make_subplots(
    rows=2,
    cols=2,
    horizontal_spacing=0.01,
    vertical_spacing=0.05,
    specs=[
        [{"type": "surface"}, {"type": "surface"}],
        [{"type": "surface"}, {"type": "surface"}],
    ],
    subplot_titles=[
        "thr₁ < thr₂ < mᵣ",
        "thr₁ < mᵣ < thr₂",
    ],
)

# thr₁ < thr₂ < mᵣ
selector = dict(col=1, row=1)
plotly_fig.add_trace(Sp_I_res1, **selector)
plotly_fig.add_trace(Sn_III_res1, **selector)
plotly_fig.add_trace(lineshape_res1, **selector)
plotly_fig.add_trace(thr_points_res1, **selector)
selector = dict(col=1, row=2)
plotly_fig.add_trace(Sp_I_res1, **selector)
plotly_fig.add_trace(Sn_II_res1, **selector)
plotly_fig.add_trace(lineshape_res1, **selector)
plotly_fig.add_trace(thr_points_res1, **selector)

# thr₁ < mᵣ < thr₂
selector = dict(col=2, row=1)
plotly_fig.add_trace(Sp_I_res2, **selector)
plotly_fig.add_trace(Sn_II_res2, **selector)
plotly_fig.add_trace(lineshape_res2, **selector)
plotly_fig.add_trace(thr_points_res2, **selector)
selector = dict(col=2, row=2)
plotly_fig.add_trace(Sp_I_res2, **selector)
plotly_fig.add_trace(Sn_III_res2, **selector)
plotly_fig.add_trace(lineshape_res2, **selector)
plotly_fig.add_trace(thr_points_res2, **selector)

plotly_fig.update_layout(
    height=600,
    margin=dict(l=0, r=0, t=20, b=0),
    showlegend=False,
)

plotly_fig.update_scenes(
    camera_center=dict(z=-0.1),
    camera_eye=dict(x=1.4, y=1.4, z=1.4),
    xaxis_range=(2.0, 5.0),
    xaxis_title_text="Re √s",
    yaxis_title_text="Im √s",
    zaxis_title_text="Im T(s)",
    zaxis_range=[-vmax, +vmax],
)
plotly_fig.show()

Complex plane widget#

Show code cell source Hide code cell source

# @title
sliders = dict(
    g01=w.FloatSlider(
        description=R"$g^{0}_1$",
        value=0.5,
        min=-2,
        max=+2,
    ),
    g02=w.FloatSlider(
        description="$g^{0}_2$",
        value=0.5,
        min=-2,
        max=+2,
    ),
    m0=w.FloatSlider(
        description="$m_0$",
        value=4,
        min=0,
        max=+6,
    ),
    T_max=w.FloatSlider(
        description=R"$T_\mathrm{max}$",
        value=1.0,
        min=0.1,
        max=6.0,
        step=0.1,
    ),
)


fig, axes = plt.subplots(
    figsize=(11, 6),
    ncols=2,
    nrows=2,
    sharex=True,
    gridspec_kw={"height_ratios": [1, 2]},
)
fig.canvas.toolbar_visible = False
fig.canvas.header_visible = False
fig.canvas.footer_visible = False
ax1d1, ax1d2, ax2d1, ax2d2 = axes.flatten()

for ax in axes[1]:
    ax.set_xlabel(R"$\mathrm{Re}\,\sqrt{s}$")
ax1d1.set_ylabel("Intensity (a.u.)")
ax2d1.set_ylabel(R"$\mathrm{Im}\,\sqrt{s}$")

ax1d1.set_title("I and II")
ax1d2.set_title("I and III")

R_color = "C4"
T1_color = "C0"
T2_color = "C3"
T3_color = "C2"


LINES = None
MESH = None
style = dict(cmap=plt.cm.coolwarm)


def plot(m0, g01, g02, T_max):
    global LINES, MESH
    local_args = args1[:-3] + (m0, g01, g02)
    T1p_res1 = T_I_func(Zp**2, *local_args)
    T2n_res1 = T_II_func(Zn**2, *local_args)
    T3n_res1 = T_III_func(Zn**2, *local_args)
    T1y = np.abs(T1p_res1[0]) ** 2
    T2y = np.abs(T2n_res1[0]) ** 2
    T3y = np.abs(T3n_res1[0]) ** 2
    if MESH is None and LINES is None:
        LINES = [
            ax1d1.axvline(m0, c=R_color, ls="dashed"),
            ax1d2.axvline(m0, c=R_color, ls="dashed"),
            ax2d1.axvline(m0, c=R_color, ls="dashed", label=R"$m_\mathrm{res}$"),
            ax2d2.axvline(m0, c=R_color, ls="dashed", label=R"$m_\mathrm{res}$"),
            ax1d1.plot(x, T1y, c=T1_color, label=R"$\left|T_\mathrm{I}\right|^2$")[0],
            ax1d1.plot(
                x, T2y, c=T2_color, label=R"$\left|T_\mathrm{II}\right|^2$", ls="dotted"
            )[0],
            ax1d2.plot(x, T1y, c=T1_color, label=R"$\left|T_\mathrm{I}\right|^2$")[0],
            ax1d2.plot(
                x,
                T3y,
                c=T3_color,
                label=R"$\left|T_\mathrm{III}\right|^2$",
                ls="dotted",
            )[0],
        ]
        MESH = [
            ax2d1.pcolormesh(X, Y, T1p_res1.imag, **style),
            ax2d1.pcolormesh(X, -Y, T2n_res1.imag, **style),
            ax2d2.pcolormesh(X, +Y, T1p_res1.imag, **style),
            ax2d2.pcolormesh(X, -Y, T3n_res1.imag, **style),
        ]
    else:
        MESH[0].set_array(T1p_res1.imag)
        MESH[1].set_array(T2n_res1.imag)
        MESH[2].set_array(T1p_res1.imag)
        MESH[3].set_array(T3n_res1.imag)
        LINES[0].set_xdata(m0)
        LINES[1].set_xdata(m0)
        LINES[2].set_xdata(m0)
        LINES[3].set_xdata(m0)
        LINES[4].set_ydata(T1y)
        LINES[5].set_ydata(T2y)
        LINES[6].set_ydata(T1y)
        LINES[7].set_ydata(T3y)
    for mesh in MESH:
        mesh.set_clim(-T_max, +T_max)
    for ax in axes[0]:
        ax.set_ylim(0, max(T1y) * 1.05)
    fig.canvas.draw()


for ax in axes[:, 1]:
    ax.set_yticks([])
for ax in axes[1]:
    ax.axhline(0, c="black", ls="dotted", lw=1)
for ax in axes[0]:
    ax.axvline(s_thr1, c="C0", ls="dotted", lw=1)
    ax.axvline(s_thr2, c="C1", ls="dotted", lw=1)
for ax in axes[1]:
    ax.axvline(s_thr1, c="C0", label=R"$\sqrt{s_\mathrm{thr1}}$", ls="dotted", lw=1)
    ax.axvline(s_thr2, c="C1", label=R"$\sqrt{s_\mathrm{thr2}}$", ls="dotted", lw=1)
ax2d1.text(0.5, +0.7, R"$T_\mathrm{I}$", color=T1_color, size=20)
ax2d1.text(0.5, -0.75, R"$T_\mathrm{II}$", color=T2_color, size=20)
ax2d2.text(0.5, +0.7, R"$T_\mathrm{I}$", color=T1_color, size=20)
ax2d2.text(0.5, -0.75, R"$T_\mathrm{III}$", color=T3_color, size=20)

output = w.interactive_output(plot, controls=sliders)
UI = w.VBox(list(sliders.values()))
fig.tight_layout()
ax1d1.legend()
ax1d2.legend()
ax2d2.legend()
display(output, UI)

Coupled channel Riemann sheets

Contents

Coupled channel Riemann sheets#

Expression definitions#

Riemann sheet I#

Matrix definition#

Parametrization#

Sheets II, III, and IV#

Visualizations#

Lineshapes (real axis)#

Complex plane (2D)#

Riemann sheets (3D)#

Complex plane widget#